��Ŀ����
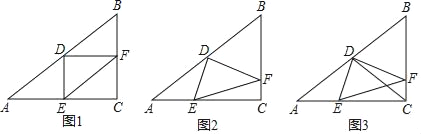
����Ŀ����ͼ����֪��ABC�У���ACB=90����AC=8��cosA=![]() ��D��AB�ߵ��е㣬E��AC����һ�㣬����DE������D��DF��DE��BC���ڵ�F������EF��
��D��AB�ߵ��е㣬E��AC����һ�㣬����DE������D��DF��DE��BC���ڵ�F������EF��
��1����ͼ1����DE��ACʱ����EF�ij���
��2����ͼ2������E��AC�����ƶ�ʱ����DFE������ֵ�Ƿ�ᷢ���仯������仯��˵���仯�����������ֲ��䣬�������DFE������ֵ��
��3����ͼ3������CD��EF�ڵ�Q������CQF�ǵ���������ʱ����ֱ��д��BF�ij���
���𰸡���1��EF=5����2�����䣬���ɼ���������3��BF�ij�Ϊ3��![]() ��
��![]() ��
��
�������������������1����cosA=![]() ������������Ǻ����Ķ���������AC=8��AE=4����Rt��EDF�У��ɹ��ɶ������DE=3����Rt��AED�У��ɹ��ɶ������EF�ij���
������������Ǻ����Ķ���������AC=8��AE=4����Rt��EDF�У��ɹ��ɶ������DE=3����Rt��AED�У��ɹ��ɶ������EF�ij���
��2������D��DH��AC��DG��BC������ֱ�Ϊ��H��G���ɣ�1���ɵ�DH=3��DG=4����֤��EDH�ס�FDG���õ�![]() ,Ȼ��������ж�����⣻
,Ȼ��������ж�����⣻
��3����QF=QC��FQ=FC��CF=CQ����������.
�⣺��1���ߡ�ACB=90����![]()
��![]() ��
��
��AC=8��
��AB=10��
��D��AB�ߵ��е㣬
��![]() ��
��
��DE��AC��
���DEA=��DEC=90����
��![]() ��
��
��AE=4��
��CE=8��4=4��
����Rt��AED��AE2+DE2=AD2��
��DE=3��
��DF��DE��
���FDE=90����
�֡ߡ�ACB=90����
���ı���DECF�Ǿ��Σ�
��DF=EC=4��
����Rt��EDF��DF2+DE2=EF2��
��EF=5
��2������
��ͼ2��

����D��DH��AC��DG��BC������ֱ�Ϊ��H��G��
�ɣ�1���ɵ�DH=3��DG=4��
��DH��AC��DG��BC��
���DHC=��DGC=90��
�֡ߡ�ACB=90����
���ı���DHCG�Ǿ��Σ�
���HDG=90����
�ߡ�FDE=90����
���HDG����HDF=��EDF����HDF��
����EDH=��FDG��
�֡ߡ�DHE=��DGF=90��
���EDH�ס�FDG��
��![]() ��
��
�ߡ�FDE=90����
��![]() ��
��
��3���ٵ�QF=QCʱ��
���QFC=��QCF��
�ߡ�EDF+��ECF=180����
���D��E��C��F�ĵ㹲Բ��
���ECQ=��DFE����DFE+��QFC=��ECQ+��QCF=��ACB=90����
����DFC=90����
�֡ߡ�ACB=90����
��![]() ��
��
��![]() ��
��
�ڵ�FQ=FCʱ��
���BCD=��CQF��
�ߵ�D��AB���е㣬
��BD=CD=![]() AB=5��
AB=5��
���BDC=��BCD��
���BCD=��FCQ����BDC=��CFQ��
���FQC�ס�DCB��
�ɢ�֪����D��E��C��F�ĵ㹲Բ��
���DEF=��DCF��
�ߡ�DQE=��FQC��
���FQC�ס�DEQ��
������FQC�ס�DEQ�ס�DCB
����Rt��EDF��![]() ��
��
����DE=3k����DF=4k��EF=5k��
�ߡ�DEF=��DCF=��CQF=��DQE��
��DE=DQ=3k��
��CQ=5��3k��
�ߡ�DEQ�ס�DCB��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�FQC�ס�DCB��
��![]() ��
��
��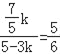 ��
��
���![]() ��
��
��![]() ��
��
��![]() ��
��
�۵�CF=CQʱ����ͼ3��

���BCD=��CQF��
�ɢ�֪��CD=BD��
���BDC=��BCD��
�ߡ�EDQ�ס�BDK��
��BC���Ͻ�ȡBK=BD=5������D��DH��BC��H��
��DH=![]() AC=4��BH=
AC=4��BH=![]() BC=3���ɹ��ɶ�����
BC=3���ɹ��ɶ�����![]() ��
��
ͬ�ڵķ����ã���CFQ�ס�EDQ��
����DE=3m����EQ=3m��EF=5m��
��FQ=2m��
�ߡ�EDQ�ס�BDK��
��![]() ��
��
��DQ=![]() m��
m��
��CQ=FC=5��![]() m��
m��
�ߡ�CQF�ס�BDK��
��![]() ��
��
��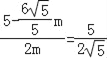 ��
��
���m=![]() ��
��
��![]() ��
��
��![]() ��
��
������CQF�ǵ���������ʱ��BF�ij�Ϊ3��![]() ��
��![]() ��
��

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�����Ŀ���������̨�����ʶ�������Ŀ������ͬѧ�ǵĶ������飬Ϊ������ѧ��������飬����������ijУ���꼶����ѧ���Ŀ����Ķ���������������飬�������������֣�ѧ�������Ķ��ı������ٵ���5����������8���������ݵ����������˲�������ͼ������ͼ��ʾ��
���������� | Ƶ���������� | Ƶ�� |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
�ϼ� | c | 1 |
��1��ͳ�Ʊ��е�a=�� ����b=�� ����c=�� ����
��2���뽫Ƶ���ֲ���ֱ��ͼ����������
��3�������б�����ѧ�������Ķ���ƽ��������
��4������У���꼶����1200��ѧ�������������У���꼶ѧ�������Ķ�7�������ϵ�������