题目内容
【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
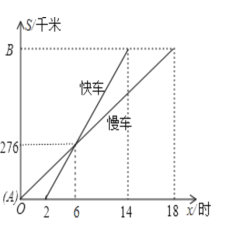
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
根据图形给出的信息求出两车的出发时间,速度等即可解答.
解:①两车在276km处相遇,此时快车行驶了4个小时,故错误.
②慢车0时出发,快车2时出发,故正确.
③快车4个小时走了276km,可求出速度为69km/h,错误.
④慢车6个小时走了276km,可求出速度为46km/h,正确.
⑤慢车走了18个小时,速度为46km/h,可得A,B距离为828km,正确.
⑥快车2时出发,14时到达,用了12小时,错误.
故答案选B.

练习册系列答案
相关题目