题目内容
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
【答案】(1)甲、乙两种玩具分别是15元/件,25元/件;(2)故商场共有四种进货方案:方案一:购进甲种玩具20件,乙种玩具28件;方案二:购进甲种玩具21件,乙种玩具27件;方案三:购进甲种玩具22件,乙种玩具26件;方案四:购进甲种玩具23件,乙种玩具25件;(3)W=﹣5m+960,最大利润860元.
【解析】
(1)设甲种玩具进价为x元/件,则乙种玩具进价为(40﹣x)元/件,根据用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解;
(2)设购进甲种玩具m件,则购进乙种玩具(48﹣m)件,根据甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,可列出不等式组求解;
(3)先列出有关总利润和进货量的一次函数关系式,然后利用一次函数的性质结合自变量的取值范围求最大值即可.
(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
根据题意,得![]() ,
,
解得x=15,
经检验x=15是原方程的解,
则40﹣x=25,
答:甲、乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具m件,则购进乙种玩具(48﹣m)件,
由题意,得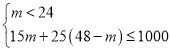 ,
,
解得20≤m<24,
∵m是整数,
∴m取20,21,22,23,
故商场共有四种进货方案:
方案一:购进甲种玩具20件,乙种玩具28件;
方案二:购进甲种玩具21件,乙种玩具27件;
方案三:购进甲种玩具22件,乙种玩具26件;
方案四:购进甲种玩具23件,乙种玩具25件;
(3)设购进甲种玩具m件,卖完这批玩具获利W元,则购进乙种玩具(48﹣m)件,
根据题意得:W=(30﹣15)m+(45﹣25)(48﹣m)=﹣5m+960,
∵比例系数k=﹣5<0,
∴W随着m的增大而减小,
∴当m=20时,有最大利润W=﹣5×20+960=860元.