��Ŀ����
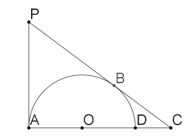
����Ŀ����ͼ������ͼ��ÿ��̨���϶�����һ���������µ��ϵĵ�1������4��̨�������α��ũ�3����2����1��0�������������ĸ�̨�������ĺͶ���ȣ�
��1��������̨���ϵ���x�Ƕ��٣�
��2����ǰ21��̨���ϵ����ĺ��Ƕ��٣�
��3�����֣�����������һ���Ĺ��ɣ���n����2�����ڵ��� ����̨���ϣ�
��4����չ�����ٻٻСͬѧһ��ֻ����1������2��̨�ף���ô���ϵ�һ��̨�ķ�����1�֣�1��1���ϵڶ���̨�ķ�����2�֣�1+1��2��2��2���ϵ�����̨�ķ�����3�֣�1+1+1��3��1+2��3��2+1��3���������ϵ����̨�ķ����������� ���֣�
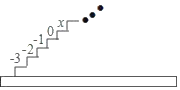
���𰸡���1�������̨���ϵ���x�ǩ�3��2��-33��3����4n��2����4��8
��������
��1������������4��������ӿɵã����ݡ������ĸ�̨�������ĺͶ���ȡ��г��������ɵ�x��
��2�����ݡ�̨���ϵ�������ÿ4��һѭ�������ɵã�
��3��̨���ϵ�������ÿ4��һѭ�������ݹ��ɿɵý��ۣ�
��4�����ݵ�һ����1��̨��2��̨��������ۿɵý��ۣ�
��1����������3��2��1+0����2��1+0+x��
x����3��
�𣺵����̨���ϵ���x�ǩ�3��
��2��������֪��̨���ϵ�������ÿ4��һѭ����
��3��2��1+0����6��
��21��4��5��1��
��5������6��+����3������33��
��ǰ21��̨���ϵ����ĺ��ǩ�33��
��3����һ����2�ڵ�2��̨���ϣ�
�ڶ�����2�ڵ�6��̨���ϣ�
��������2�����ڵ�10��̨���ϣ�
��
��n����2�����ڵڣ�4n��2����̨���ϣ�
�ʴ�Ϊ��4n��2����
��4���ϵ����̨�ķ�����1+1+1+1+1��5��1�֣�
1+1+1+2��5��1+2+2��5��1+2+1+1��5��1+1+2+1��5��4�֣�
2+2+1��5��2+1+2��5��2+1+1+1��5��3�֣�
��1+4+3��8�֣�
�����ϵ����̨�ķ���������8�֣�
�ʴ�Ϊ8��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�