题目内容
【题目】如图,在△BDE中,∠BDE=90°,BD=4![]() , 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为
, 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 
【答案】(3,2![]() )
)
【解析】解:如图,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F.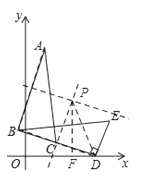
∵点C在BD上,
∴点P到AB、BD的距离相等,都是![]() BD,即
BD,即![]() ×4
×4![]() =2
=2![]() ,
,
∴∠PDB=45°,
PD=![]() ×2
×2![]() =4,
=4,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=![]() PD=
PD=![]() ×4=2,
×4=2,
∵点D的坐标是(5,0),
∴OF=OD﹣DF=5﹣2=3,
由勾股定理得,PF=![]()
∴旋转中心的坐标为(3,2![]() ).
).
故答案为:(3,2![]() ).
).
根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=![]() PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目