题目内容
【题目】如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为 .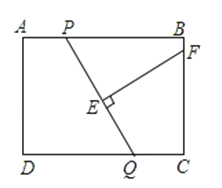
【答案】y=![]() x﹣
x﹣![]()
【解析】解:连接PF,QF,
∵线段EF是PQ的垂直平分线,
∴PF=QF,
∵在矩形ABCD中,AB=8,AD=6,
∴BC=AD=6,
∵AP=x,BF=y,
∴PB=8﹣x,CF=6﹣y,
∵CQ=AP=x,
∴在Rt△PBF中,PF2=PB2+BF2=(8﹣x)2+y2 , 在Rt△CQF中,QF2=CF2+CQ2=(6﹣y)2+x2 ,
∴(8﹣x)2+y2=(6﹣y)2+x2 ,
即y=![]() x﹣
x﹣![]() .
.
故答案为:y=![]() x﹣
x﹣![]() .
. 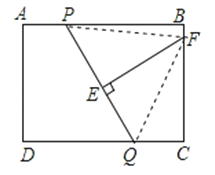
首先连接PF,QF,由线段EF是PQ的垂直平分线,可得PF=QF,又由在矩形ABCD中,AB=8,AD=6,AP=x,BF=y,且AP=CQ,可得方程:(8﹣x)2+y2=(6﹣y)2+x2 , 继而求得答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目