题目内容
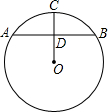
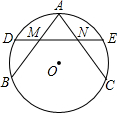
如图所示,D、E分别是弧
、
的中点,DE交AB于M、交AC于N.求证:AM=AN.
 |
| AB |
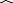 |
| AC |

证明:连接DO,EO,∵D是
中点,E是
中点,
∴OD⊥AB,OE⊥AC.
又∵∠EDO=∠DEO,
∴∠DMB=180°-∠EDO-90°,∠ENC=180°-90°-∠DEO.
∴∠DMB=∠ENC.
而∠AMN=∠DMB,∠ENC=∠ANM,
∴∠AMN=∠ANM.
∴AM=AN.

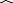 |
| AB |
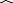 |
| AC |
∴OD⊥AB,OE⊥AC.
又∵∠EDO=∠DEO,
∴∠DMB=180°-∠EDO-90°,∠ENC=180°-90°-∠DEO.
∴∠DMB=∠ENC.
而∠AMN=∠DMB,∠ENC=∠ANM,
∴∠AMN=∠ANM.
∴AM=AN.


练习册系列答案
相关题目