题目内容
【题目】数学课上,小白遇到这样一个问题:
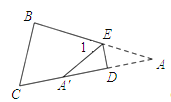
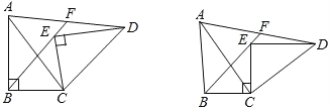
如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() ,求证
,求证![]() ;
;
在此问题的基础上,老师补充:
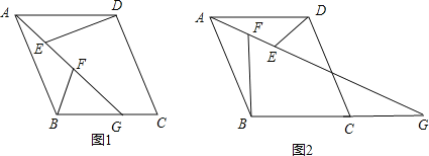
过点![]() 作
作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试探究线段
,试探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
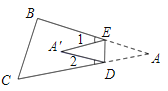
小白通过研究发现,![]() 与
与![]() 有某种数量关系;
有某种数量关系;
小明通过研究发现,将三条线段中的两条放到同一条直线上,即“截长补短”,再通过进一步推理,可以得出结论.
阅读上面材料,请回答下面问题:
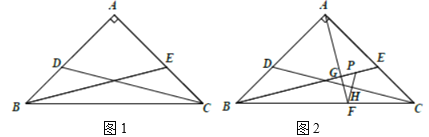
(1)求证![]() ;
;
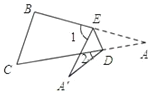
(2)猜想![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
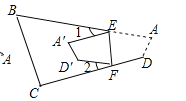
(3)探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)利用SAS证明![]() 可得结论;
可得结论;
(2)设![]() ,推出
,推出![]() ,
,![]() ,即可证明
,即可证明![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,证明△ABE≌△CAM,得出
,证明△ABE≌△CAM,得出![]() 和
和![]() ,从而证明△NFC≌△MFC,得到
,从而证明△NFC≌△MFC,得到![]() 和
和![]() ,可得PN=PE,从而得出BP=AF+PF.
,可得PN=PE,从而得出BP=AF+PF.
解:(1)∵在△ABE和△ACD中,
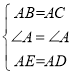 ,
,
![]() (SAS),
(SAS),
![]() ;
;
(2)设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在△ABE和△CAM中,
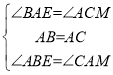 ,
,
![]() (ASA),
(ASA),
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() (ASA),
(ASA),
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
![]() .
.

练习册系列答案
相关题目