题目内容
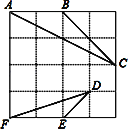
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
【答案】(1)135,![]() ;(2)△ABC∽△DEF,证明见解析
;(2)△ABC∽△DEF,证明见解析
【解析】
(1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△ACH中利用勾股定理即可求出AC的长;
(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.
(1)∵△BCG是等腰直角三角形,∴∠GBC=45°.
∵∠ABG=90°,∴∠ABC=∠GBC+∠ABG=45°+90°=135°.
在Rt△AHC中,∵AH=4,CH=2,∴AC![]() .
.
故答案为:135,![]() ;
;
(2)△ABC∽△DEF.理由如下:
在4×4的正方形方格中,∵∠ABC=∠DEF=135°,∴∠ABC=∠DEF.
∵AB=2,BC=2![]() ,FE=2,DE
,FE=2,DE![]() ,∴
,∴![]() ,∴△ABC∽△DEF.
,∴△ABC∽△DEF.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目