Question

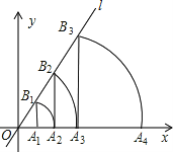
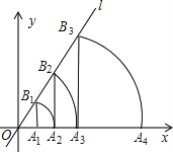
【题目】在直角坐标系中，直线l为y=x，过点A1（1，0）作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画弧交x轴于点A2，再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3…按照这样的作法进行下去，则点A20的坐标是______．

Answer 1

【答案】（219，0）

【解析】

根据题意，由(1，0)和直线关系式y=x，可以求出点B1的坐标，在Rt△OA1B1中，根据勾股定理，可以求出OB1的长；再根据OB1=OA2确定A2点坐标，同理可求出A3、A4、A5……，然后再找规律，得出An的坐标，从而求得点A20的坐标．

当时，，即A1B1=，

在Rt△OA1B1中，由勾股定理得OB1=2，

∵OB1=OA2，

∴A2 (2，0)

同理可求：A3(4，0)、A4(8，0)、A5(16，0)……

由点：A1(1，0)、A2(2，0)、A3(4，0)、A4(8，0)、A5(16，0)……

即：A1(20，0)、A2(21，0)、A3(22，0)、A4(23，0)、A5(24，0)……可得An(2n-1，0)

∴点A20的坐标是(219，0)，

故答案为：(219，0)．