题目内容
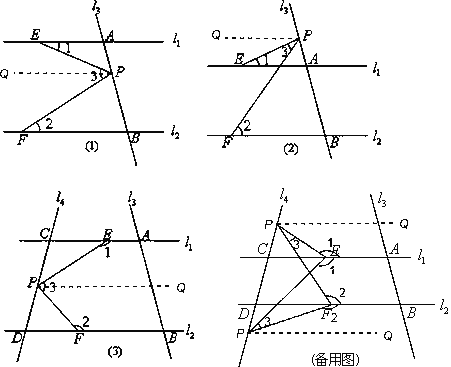
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.

(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明;
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系.
【答案】(1)证明见解析;(2)∠3=∠2﹣∠1;证明见解析;(3)∠3=360°﹣∠1﹣∠2.证明见解析;(4)当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.
【解析】
此题四个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
解:(1)证明:过P作PQ∥l1∥l2,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)∠3=∠2﹣∠1;
证明:过P作直线PQ∥l1∥l2,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
(3)∠3=360°﹣∠1﹣∠2.
证明:过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
(4)过P作PQ∥l1∥l2;
①当P在C点上方时,
同(2)可证:∠3=∠DFP﹣∠CEP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠DFP﹣∠CEP+∠2﹣∠1=0,
即∠3=∠1﹣∠2.
②当P在D点下方时,
∠3=∠2﹣∠1,解法同上.
综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.