题目内容
【题目】长方形![]() 为平面直角坐标系的原点,
为平面直角坐标系的原点,![]() 点
点![]() 在第三象限.
在第三象限.
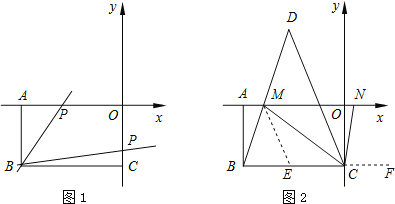
(1)如图1,若过点![]() 的直线
的直线![]() 与长方形
与长方形![]() 的边交于点
的边交于点![]() 且将长方形
且将长方形![]() 的面积分为
的面积分为![]() 两部分,求点
两部分,求点![]() 的坐标;
的坐标;

(2)如图2,![]() 为
为![]() 轴负半轴上一点,且
轴负半轴上一点,且![]() 是
是![]() 轴正半轴上一动点,
轴正半轴上一动点,![]() 的平分线
的平分线![]() 交
交![]() 的延长线于点
的延长线于点![]() 在点
在点![]() 运动的过程中,
运动的过程中,![]() 的值是否变化?若不变求出其值;若变化,请说明理由.
的值是否变化?若不变求出其值;若变化,请说明理由.

【答案】(1)点P的坐标为(-3,0)或(0,-![]() );(2)
);(2)![]() .
.
【解析】
(1)利用长方形OABC的面积分为1:4两部分,得出等式求出AP的长,即可得出P点坐标,再求出PC的长,即可得出OP的长,进而得出答案;
(2)首先求出∠MCF=2∠CMB,即可得出∠CNM=∠AMC-∠NCM=2∠BMC-2∠DCM=2∠BMC-2∠EMC=2∠D,得出答案.
(1)如图1,若过点B的直线BP与边OA交于点P,依题意可知:![]() ×AB×AP=
×AB×AP=![]() ×OA×OC,
×OA×OC,
即![]() ×3×AP=
×3×AP=![]() ×5×3,
×5×3,
∴AP=2
∵OA=5,
∴OP=3,
∴P(-3,0),
若过点B的直线BP与边OC交于点P,依题意可知:![]() ×BC×PC=
×BC×PC=![]() ×OA×OC,
×OA×OC,
即![]() ×5×PC=
×5×PC=![]() ×5×3,
×5×3,
∴PC=![]()
∵OC=3,
∴OP=![]() ,
,
∴P(0,-![]() ).
).
综上所述,点P的坐标为(-3,0)或(0,-![]() ).
).
(2)如图2,延长BC至点F,
∵四边形OABC为长方形,
∴OA∥BC.
∴∠CBM=∠AMB,∠AMC=∠MCF.
∵∠CBM=∠CMB,
∴∠MCF=2∠CMB.
过点M作ME∥CD交BC于点E,
∴∠EMC=∠MCD.
又∵CD平分∠MCN,
∴∠NCM=2∠EMC.
∴∠D=∠BME=∠CMB-∠EMC,
∠CNM=∠AMC-∠NCM=2∠BMC-2∠DCM=2∠BMC-2∠EMC=2∠D,
∴![]() .
.

【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.