题目内容
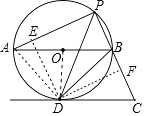
【题目】如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合), ![]() =
= ![]() ,过点D作⊙O的切线交PB的延长线于点C.
,过点D作⊙O的切线交PB的延长线于点C. 
(1)试证明AB∥CD;
(2)填空: ①当BP=1cm时,PD=cm;
②当BP=cm时,四边形ABCD是平行四边形.
【答案】
(1)证明:连接OD.
∵CD是⊙O的切线,
∴OD⊥CD,
∵ ![]() =
= ![]() ,
,
∴∠AOD=∠BOD=90°,
∴OD⊥AB,
∴AB∥CD.
(2)![]() +
+ ![]() ;
; ![]()
【解析】(2)解:①作DE⊥AP于E,DF⊥PC于F.
∵ ![]() =
= ![]() ,
,
∴∠APD=∠DPB,
∴DE=DF,
∵AB是直径,
∴∠APB=90°,
∴∠EPD=∠FPD=45°,易知四边形PEDF是正方形,
∵AD=BD,DE=DF,
∴Rt△DEA≌Rt△DFB,
∴AE=BF,
在Rt△PAB中,∵AB=2cm,PB=1cm,
∴PA= ![]() =
= ![]() ,
,
∴PA+PB=PE+AE+PF﹣BF=2PE=1+ ![]() ,
,
∴PD= ![]() PE=(
PE=( ![]() +
+ ![]() )cm.
)cm.
所以答案是 ![]() +
+ ![]() .②当P是
.②当P是 ![]() 中点时,DC=2OB=AB,
中点时,DC=2OB=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形.
易知BD= ![]() OB=
OB= ![]() cm,
cm,
所以答案是 ![]() .
.

【考点精析】关于本题考查的平行四边形的判定和切线的性质定理,需要了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?