题目内容
【题目】已知抛物线y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)与x轴分别交于A(x1 , 0)、
B(x2 , 0)两点,直线y2=2x+t经过点A.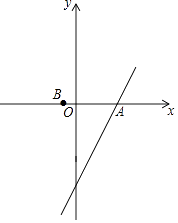
(1)已知A、B两点的横坐标分别为3、﹣1.
①当a=1时,直接写出抛物线y1和直线y2相应的函数表达式;
②如图,已知抛物线y1在3<x<4这一段位于直线y2的下方,在5<x<6这一段位于直线y2的上方,求a的取值范围;
(2)若函数y=y1+y2的图象与x轴仅有一个公共点,探求x2﹣x1与a之间的数量关系.
【答案】
(1)解:①∵已知抛物线y1=a(x﹣x1)(x﹣x2)经过A(x1,0)、B(x2,0)两点,当a=1,
∴y1=(x﹣3)(x+1),
∵直线y2=2x+t经过点A,
∴0=2×3+t,
解得:t=﹣6,
∴y2=2x﹣6;
②设y1=a(x﹣3)(x+1),
由题意可得,当x=4时,y1=5a<2,
∴a< ![]() ,
,
当x=5时,y1=12a>4,
∴a> ![]() ,
,
∴ ![]() a<
a< ![]()
(2)解:∵直线y2过点A(x1,0),
∴0=2x1+t,∴t=﹣2x1,
∴y=y1+y2=a(x﹣x1)(x﹣x2)+2x﹣2x1=(x﹣x1)[a(x﹣x1)+2]
∴方程的根为x1,x2﹣ ![]() ,
,
∵函数y的图象与x轴仅有一个公共点,
∴x1=x2﹣ ![]() ,
,
∴x2﹣x1= ![]()
【解析】
(1)①根据已知条件得出当a=1时,得到y1=(x﹣3)(x+1),由于直线y2=2x+t经过点A,得到方程0=2×3+t,得到t=﹣6,
于是得到结论;②设y1=a(x﹣3)(x+1),根据题意得出不等式即可得出结论;(2)根据已知条件得到y=y1+y2=a(x﹣x1)(x﹣x2)+2x﹣2x1=(x﹣x1)[a(x﹣x1)+2],根据函y的图像与x轴仅有一个公共点,于是得到结论。
【考点精析】通过灵活运用确定一次函数的表达式和抛物线与坐标轴的交点,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.

【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
【题目】某水果店去年3至8月销售吐鲁番葡萄、哈密瓜的情况如下表:
3月 | 4月 | 5月 | 6月 | 7月 | 8月 | |
吐鲁番葡萄(单位:百公斤) | 4 | 8 | 5 | 8 | 10 | 13 |
哈密瓜(单位:百公斤) | 8 | 7 | 9 | 7 | 10 | 7 |
(1)请你根据以上数据填写下表:
平均数/百公斤 | 方差 | |
吐鲁番葡萄 | 8 | 9 |
哈密瓜 |
(2)请你根据上述信息,对这两种水果在去年3月份至8月份的销售情况进行分析.