题目内容
某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表表示:
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出与之间的函数关系式:_____;
(2)每台护眼灯可获利z(元)关于等级x(级)的函数关系式:______;
(3)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
| 等级(x级) | 一级 | 二级 | 三级 | … |
| 生产量(y台/天) | 78 | 76 | 74 | … |
(2)每台护眼灯可获利z(元)关于等级x(级)的函数关系式:______;
(3)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
(1)y=-2x+80;(2)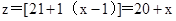 ;(3)1800元.
;(3)1800元.
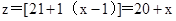 ;(3)1800元.
;(3)1800元.试题分析:(1)由于护眼灯每天的生产量y(台)是等级x(级)的一次函数,所以可设y=kx+b,再把代入,运用待定系数法即可求出y与x之间的函数关系式;
(2)根据“一级产品每台可获利21元,每提高一个等级每台可多获利润1元”即可直接写出答案;
(3)设工厂生产x等级的护眼灯时,获得的利润为w元.由于等级提高时,带来每台护眼灯利润的提高,同时销售量下降.而x等级时,每台护眼灯的利润为[21+1(x-1)]元,销售量为y元,根据:利润=每台护眼灯的利润×销售量,列出w与x的函数关系式,再根据函数的性质即可求出最大利润.
试题解析:
(1)由题意,设y=kx+b.
把(1,78)、(2,76)代入,得,解得,
∴y与x之间的函数关系式为y=-2x+80.故答案为y=-2x+80;
(2)∵一级产品每台可获利21元,每提高一个等级每台可多获利润1元
∴每台护眼灯可获利z(元)关于等级x(级)的函数关系式:;
(3)设工厂生产x等级的护眼灯时,获得的利润为w元.
由题意,有w=[21+1(x-1)]y
=[21+1(x-1)](-2x+80)
=-2(x-10)2+1800,
所以当x=10时,可获得最大利润1800元.
故若工厂将当日所生产的护眼灯全部售出,工厂应生产十级的护眼灯时,能获得最大利润,最大利润是1800元.

练习册系列答案
相关题目
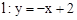 与y轴交于点A,抛物线
与y轴交于点A,抛物线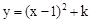 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线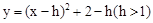 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C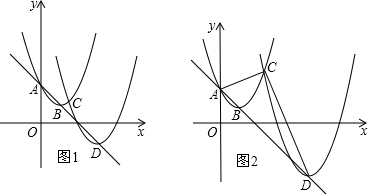
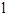 的理由;
的理由;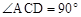 ,求m的值.
,求m的值.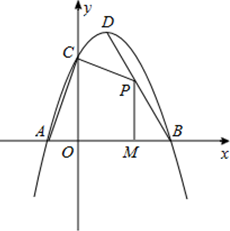
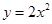 的图象向上平移1个单位,则平移后的抛物线的解析式为( )
的图象向上平移1个单位,则平移后的抛物线的解析式为( )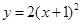
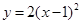
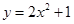
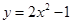
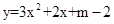 的图象经过原点,则m= .
的图象经过原点,则m= . 与双曲线
与双曲线 的交点A的横坐标是1,则关于
的交点A的横坐标是1,则关于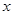 的不等式
的不等式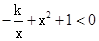 的解集是( )
的解集是( )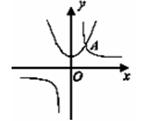
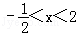 时,y<0;
时,y<0;