题目内容
【题目】已知关于x的一元二次方程x2－（2k＋1）x＋k2＋2k＝0有两个实数根x1 ， x2 ．
（1）求实数k的取值范围；
（2）是否存在实数k，使得x1·x2－x12－x22≥0成立？若存在，请求出k的值；若不存在，请说明理由．
【答案】
（1）解： 
，解得 
（2）解：由 
，
由根与系数的关系可得： 
代入得： 
，
化简得： 
，
得 
.
由于 
的取值范围为 ，
故不存在k使 
。
【解析】（1）根据题意可知原方程有两个实数根，得出b2-4ac≥0，列不等式求解即可。
（2）先将x1·x2－x12－x22转化为 3x1x2（x1+x2）2，再利用根与系数的关系求出x1+x2和x1x2，然后代入建立关于k的不等式，求出不等式的解集，即可得出结果。
【考点精析】根据题目的已知条件，利用求根公式和根与系数的关系的相关知识可以得到问题的答案，需要掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根；一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商．
活力课时同步练习册系列答案
学业测评一课一测系列答案
【题目】在硬地上抛掷一枚图钉，通常会出现两种情况：
下面是小明和同学做“抛掷图钉实验”获得的数据：
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
（1）填写表中的空格；
（2）画出该实验中，抛掷图钉钉尖不着地频率的折线统计图；
（3）根据“抛掷图钉实验”的结果，估计“钉尖着地”的概率为 ．
【题目】某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表
x单位：台） | 10 | 20 | 30 |
y（单位：万元/台） | 60 | 55 | 50 |
（1）求y与x之间的函数关系式；
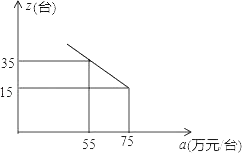
（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系．
①该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润．（注：利润＝售价﹣成本）
②若该厂每月生产的这种机器当月全部售出，则每个月生产多少台这种机器才能使每台机器的利润最大？
