题目内容
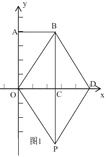
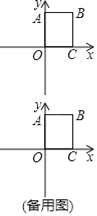
【题目】如图，在平面直角坐标系中，四边形OABC为矩形，点A（0，8），C（6，0）．动点P从点B出发，以每秒1个单位长的速度沿射线BC方向匀速运动，设运动时间为t秒．
（1）当t= s时，以OB、OP为邻边的平行四边形是菱形；
（2）当点P在OB的垂直平分线上时，求t的值；
（3）将△OBP沿直线OP翻折，使点B的对应点D恰好落在x轴上，求t的值．
【答案】（1）16；（2）t=
；（3）满足条件的t的值为5s或20s．
【解析】试题分析：（1）先有菱形的性质得出PC=BC=8，进而得出BP=16即可得出结论；
（2）由线段的垂直平分线的性质得出PO=PB=t，再利用勾股定理即可求出结论；
（3）分点P在x轴坐标轴和负半轴上，利用勾股定理即可建立方程求解．
试题解析：（1）如图1，
∵A（0，8），∴OA=8，C（6，0），∴OC=6，
∵四边形OABC是矩形，∴BC=OA=8，
∵以OB、OP为邻边的平行四边形是菱形，∴CP=BC=OA=8，
∴BP=BC+CP=16，t=16÷1=16s，
故答案为16；
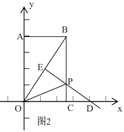
（2）如图2，∵点P是OB的垂直平分线上，∴PO=PB=t，∴PC=BC﹣PB=8﹣t，
在Rt△POC中，OC=6，根据勾股定理得，OC2+PC2=OP2，∴62+（8﹣t）2=t2，
∴t=
；
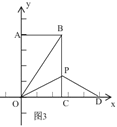
（3）当点P在x轴的坐标轴上时，如图3，
由折叠知，△OBP≌△ODP，∴PD=PB=t，OD=OB=
=10，∴CD=OD﹣OC=4，
在Rt△PCD中，CD=4，PC=BC﹣PB=8﹣t，PD=t，
根据勾股定理得，PC2+CD2=PD2，∴42+（8﹣t）2=t2，∴t=5，
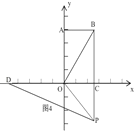
当点P在x轴负半轴上时，如图4，
由折叠知，PB=PD=t，OD=OB=10，∴CD=OD+OC=16，PC=t﹣8，
在Rt△PCD中，根据勾股定理得，PC2+CD2=PD2，∴（t﹣8）2+162=t2，∴t=20，
即：满足条件的t的值为5s或20s．
