题目内容
【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
x单位:台) | 10 | 20 | 30 |
y(单位:万元/台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式;
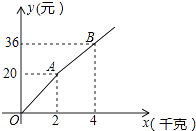
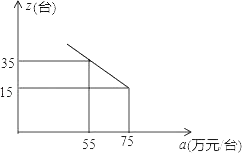
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.
①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?
【答案】(1)y=-0.5x+65(10≤x≤70,且为整数);(2)①200万元;②10.
【解析】
(1)根据函数图象和图象中的数据可以求得y与x的函数关系式;
(2)①根据函数图象可以求得z与a的函数关系式,然后根据题意可知x=40,z=40,从而可以求得该厂第一个月销售这种机器的总利润;
②根据题意可以得到每台的利润和台数之间的关系式,从而可以解答本题.
解:(1)设y与x的函数关系式为y=kx+b,
![]() ,得
,得![]() ,
,
即y与x的函数关系式为y=-0.5x+65(10≤x≤70,且为整数);
(2)①设z与a之间的函数关系式为z=ma+n,
![]() ,得
,得![]() ,
,
∴z与a之间的函数关系式为z=-a+90,
当z=40时,40=-a+90,得a=50,
当x=40时,y=-0.5×40+65=45,
40×50-40×45
=2000-1800
=200(万元),
答:该厂第一个月销售这种机器的总利润为200万元;
②设每台机器的利润为w万元,
W=(-x+90)-(-0.5x+65)=-![]() x+25,
x+25,
∵10≤x≤70,且为整数,
∴当x=10时,w取得最大值,
答:每个月生产10台这种机器才能使每台机器的利润最大.
故答案为:(1)y=-0.5x+65(10≤x≤70,且为整数);(2)①200万元;②10.