题目内容
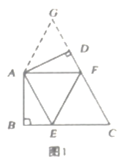
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,对角线
,对角线![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形;
是矩形;
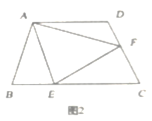
![]() 如图
如图![]() ,若动点
,若动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
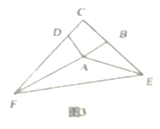
![]() 如图
如图![]() ,若点
,若点![]() 在对角线
在对角线![]() 上,
上,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动至点
运动至点![]() 止.设点
止.设点![]() 运动了
运动了![]() 秒,请你探索:从运动开始,经过多少时间,以点
秒,请你探索:从运动开始,经过多少时间,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?请求出所有可能的结果.
为顶点的三角形是等腰三角形?请求出所有可能的结果.

【答案】(1)详见解析;(2)![]() ;(3)从运动开始,经过
;(3)从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
【解析】
(1)先判定四边形ABCD是平行四边形,再根据∠B=90°,得出四边形ABCD是矩形;
(2)先过Q作QM⊥BC于M点,AP与BQ交于点N,判定△ABP∽△BMQ,得出![]() =
=![]() ,即
,即![]() =
=![]() ,求得t的值即可;
,求得t的值即可;
(3)分为三种情况讨论:当CQ=CP=4cm时,当PQ=CQ=4cm时,当QP=CP时,分别根据等腰三角形的性质,求得BP的长,进而得到t的值.
![]() 证明:∵
证明:∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形;
是矩形;
![]() 如图,过
如图,过![]() 作
作![]() 于
于![]() 点,
点,![]() 与
与![]() 交于点
交于点![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
![]() 分为三种情况:
分为三种情况:
①如图![]() 所示,当
所示,当![]() 时,
时,![]() ,
,

∴![]() 秒;
秒;
②如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() 秒;
秒;
③如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,![]() ,
,
∵![]() ,
,

∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒.
秒.
综上所述,从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.

练习册系列答案
相关题目