ЬтФПФкШн
ЁОЬтФПЁПдФЖСРэНтЃКЮвУЧжЊЕРЃЌБШНЯСНЪ§ЃЈЪНЃЉДѓаЁгаКмЖрЗНЗЈЃЌЁАзїВюЗЈЁБЪЧГЃгУЕФЗНЗЈжЎвЛЃЌЦфдРэЪЧВЛЕШЪНЃЈЛђЕШЪНЃЉЕФаджЪЃКШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛШє
ЃЛШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛШє
ЃЛШє![]() ЃЌдђ
ЃЌдђ![]() .
.
Р§ЃКвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
жЄУїЃК![]()
![]() .
.
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() .
.
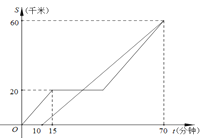
ЃЈ1ЃЉВйзїИажЊЃКБШНЯДѓаЁЃК
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ______
______![]() ЃЛ
ЃЛ
Ђк![]() ______
______![]() .
.
ЃЈ2ЃЉРрБШЬНОПЃКвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЪддЫгУЩЯЪіЗНЗЈБШНЯ
ЃЌЪддЫгУЩЯЪіЗНЗЈБШНЯ![]() ЁЂ
ЁЂ![]() ЕФДѓаЁЃЌВЂЫЕУїРэгЩ.
ЕФДѓаЁЃЌВЂЫЕУїРэгЩ.
ЃЈ3ЃЉгІгУЭиеЙЃКвбжЊ![]() ЃЌ
ЃЌ![]() ЮЊЦНУцжБНЧзјБъЯЕжаЕФСНЕуЃЌаЁУїШЯЮЊЃЌЮоТл
ЮЊЦНУцжБНЧзјБъЯЕжаЕФСНЕуЃЌаЁУїШЯЮЊЃЌЮоТл![]() ШЁКЮжЕЃЌЕу
ШЁКЮжЕЃЌЕу![]() ЪМжедкЕу
ЪМжедкЕу![]() ЕФЩЯЗНЃЌаЁУїЕФВТЯыЖдТ№ЃПЮЊЪВУДЃП
ЕФЩЯЗНЃЌаЁУїЕФВТЯыЖдТ№ЃПЮЊЪВУДЃП
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() ;(2)M<NЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉаЁУїЕФВТЯыЪЧЖдЕФЃЌРэгЩМћНтЮі
;(2)M<NЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉаЁУїЕФВТЯыЪЧЖдЕФЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнВЛЕШЪНЕФаджЪМДПЩЕУГіД№АИЃЛЂкИљОнЭъШЋЦНЗНЙЋЪНМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉСНЪНЯрМѕМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉСНЕуКсзјБъЯрЭЌЃЌБШНЯзнзјБъЕФДѓаЁМДПЩЕУГіД№АИ.
ЃЈ1ЃЉЂйЁп![]()
Ёрa+b<0ЃЌa-b<0
Ёр![]() <0
<0
ЙЪД№АИЮЊЃК<.
Ђк![]()
ЙЪД№АИЮЊЃКЁн.
ЃЈ2ЃЉ![]() ЃЌРэгЩЃКЩш
ЃЌРэгЩЃКЩш![]() ЃЌ
ЃЌ
дђ![]()
![]() ЃЌ
ЃЌ
Ёр![]() .
.
ЃЈ3ЃЉаЁУїЕФВТЯыЪЧЖдЕФЃЌРэгЩШчЯТЃК![]() ЃЌ
ЃЌ
ЫљвдЃЌЮоТл![]() ШЁКЮжЕЃЌЕу
ШЁКЮжЕЃЌЕу![]() ЖМдкЕу
ЖМдкЕу![]() ЕФЩЯЗНЃЌМДаЁУїЕФЙлЕуе§ШЗ.
ЕФЩЯЗНЃЌМДаЁУїЕФЙлЕуе§ШЗ.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПМзЁЂввСНЮЛЭЌбЇВЮМгЪ§бЇзлКЯЫижЪВтЪдЃЌИїЯюГЩМЈШчЯТЃЈЕЅЮЛЃКЗжЃЉ
Ъ§гыДњЪ§ | ПеМфгыЭМаЮ | ЭГМЦгыИХТЪ | злКЯгыЪЕМљ | |
бЇЩњМз | 90 | 94 | 86 | 90 |
бЇЩњвв | 94 | 82 | 93 | 91 |
ЃЈ1ЃЉЗжБ№МЦЫуМзЁЂввГЩМЈЕФЦНОљЪ§КЭЗНВюЃЛ
ЃЈ2ЃЉШчЙћЪ§гыДњЪ§ЁЂПеМфгыЭМаЮЁЂЭГМЦгыИХТЪЁЂзлКЯгыЪЕМљЕФГЩМЈАД3ЃК3ЃК2ЃК2МЦЫуЃЌФЧУДМзЁЂввЕФЪ§бЇзлКЯЫижЪГЩМЈЗжБ№ЮЊЖрЩйЗжЃП