Question

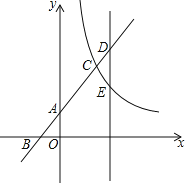
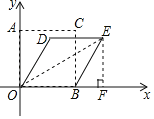
【题目】边长为4的正方形AOBC在坐标系中的位置如图所示，若OB边保持不动，推动AOBC向右倾斜30°得四边形DOBE，则点E的坐标为（　　）

A.（5，4）B.（6，2）C.（6，3）D.（4+2，5）

Answer 1

【答案】B

【解析】

由正方形的性质得出OA＝OB＝BC＝4，进而求得∠DOB＝60°，BE＝BC＝4，根据平行线的性质得出∠EBF＝∠DOB＝60°，解直角三角形求得BF＝2，EF＝2，即可求得E的坐标．

解：边长为4的正方形AOBC中，OA＝OB＝BC＝4，

∵∠AOD＝30°，

∴∠DOB＝60°，BE＝BC＝4，

∵OD∥BE，

∴∠EBF＝∠DOB＝60°，

∴BF＝BF＝2，EF＝BF＝2，

∴OF＝4+2＝6，

∴E（6，2）．

故选：B．