��Ŀ����
����Ŀ��ij�ֹ�ҵԭ�ϣ��ײֿ���12�֣��Ҳֿ���6�֣�����Ӽס������ֿ⽫���ֹ�ҵԭ�Ϸֱ����A����10�֣�B����8�֣���֪�Ӽײֿ����1��ԭ�ϵ�A��B���������˷ѷֱ���40Ԫ��80Ԫ�����Ҳֿ����1��ԭ�ϵ�A��B���������˷ѷֱ���30Ԫ��50Ԫ��
��1�������˷�Ϊ900Ԫ����Ӽײֿ���˵�A������ԭ��Ϊ���ٶ֣�
��2��Ҫʹ���˷���ͣ�Ӧ��ΰ��ŵ��˷�����
���𰸡���1���ײֿ���˵�A������ԭ��Ϊ8�֣���2���Ӽײֿ���˵�A������ԭ��Ϊ10�֣������B������ԭ��2�֣��Ҳֿ����A����ԭ��0�֣�����B����ԭ��Ϊ6�֣�
��������
��1����Ӽײֿ���˵�A������ԭ��Ϊx�֣������B������12��x���֣��Ҳֿ����A������10��x���֣�����B����[6����10��x��]�֣��ٸ��ݵ�������������һ�ֵ��˷ѣ���������˷Ѽ��ɣ�
��2�����ݵ�����ԭ��Ϊ�Ǹ����ɵ�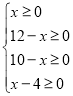 ,�ٽⲻ��ʽ��ɵ�x��ȡֵ��Χ�����������˷Ѽ���
,�ٽⲻ��ʽ��ɵ�x��ȡֵ��Χ�����������˷Ѽ���
�⣺��1����Ӽײֿ���˵�A������ԭ��Ϊx��
40x+80��12��x��+30��10��x��+50��x��4����900
��ã�x��8
����Ӽײֿ���˵�A������ԭ��Ϊ8��
��2�����ݵ�����ԭ��Ϊ�Ǹ����ɵ�: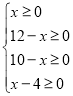 ��4��x��10
��4��x��10
�����˷�ΪyԪ����������ã�y��40x+80��12��x��+30��10��x��+50��x��4������20x+1060
�ߩ�20��0��y��x�����������
�൱x��10ʱ��y���
���Ӽײֿ���˵�A������ԭ��Ϊ10�֣������B������ԭ��2�֣��Ҳֿ����A����ԭ��0�֣�����B����ԭ��Ϊ6��.