题目内容
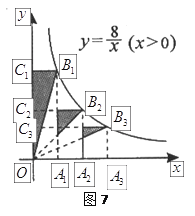
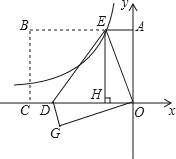
【题目】如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8![]() .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=
.把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=![]() 图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
【答案】-2![]() 2
2![]()
【解析】
连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,可通过三角形全等证得BO与ED的交点就是ED的中点F,由相似三角形的性质可得S△OGF=![]() S△OCB,根据反比例函数比例系数的几何意义可求出k,从而求出S△OAE,进而可以得到AB=4AE,即BE=3AE.由轴对称的性质可得OE=BE,从而得到OE=3AE,也就有AO=2
S△OCB,根据反比例函数比例系数的几何意义可求出k,从而求出S△OAE,进而可以得到AB=4AE,即BE=3AE.由轴对称的性质可得OE=BE,从而得到OE=3AE,也就有AO=2![]() AE,根据△OAE的面积可以求出AE,OA的值.易证四边形OAEH为矩形,从而得到EH=OA,就可求出EH的值.
AE,根据△OAE的面积可以求出AE,OA的值.易证四边形OAEH为矩形,从而得到EH=OA,就可求出EH的值.
解:连接BO与ED交于点Q,过点Q作QN⊥x轴,垂足为N,如图所示,

∵矩形OABC沿DE翻折,点B与点O重合,
∴BQ=OQ,BE=EO.
∵四边形OABC是矩形,
∴AB∥CO,∠BCO=∠OAB=90°.
∴∠EBQ=∠DOQ.
在△BEQ和△ODQ中,
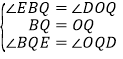 .
.
∴△BEQ≌△ODQ(ASA).
∴EQ=DQ.
∴点Q是ED的中点.
∵∠QNO=∠BCO=90°,
∴QN∥BC.
∴△ONQ∽△OCB.
∴![]() .
.
∴S△ONQ=![]() S△OCB.
S△OCB.
∵S矩形OABC=8![]() ,
,
∴S△OCB=S△OAB=4![]() .
.
∴S△ONQ=![]() .
.
∵点F是ED的中点,
∴点F与点Q重合.
∴S△ONF=![]() .
.
∵点F在反比例函数y=![]() 上,
上,
∴![]() =
=![]() .
.
∵k<0,
∴k=﹣2![]() .
.
∴S△OAE=![]() =
=![]() .
.
∵S△OAB=4![]() ,
,
∴AB=4AE.
∴BE=3AE.
由轴对称的性质可得:OE=BE.
∴OE=3AE.OA=![]() =2
=2![]() AE.
AE.
∴S△OAE=![]() AOAE=
AOAE=![]() ×2
×2![]() AE×AE=
AE×AE=![]() .
.
∴AE=1.
∴OA=2![]() ×1=2
×1=2![]() .
.
∵∠EHO=∠HOA=∠OAE=90°,
∴四边形OAEH是矩形.
∴EH=OA=2![]() .
.
故答案分别为:﹣2![]() 、2
、2![]() .
.

 培优好卷单元加期末卷系列答案
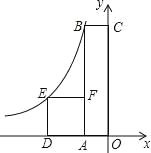
培优好卷单元加期末卷系列答案【题目】如图1,AB为半圆O的直径,半径的长为4cm,点C为半圆上一动点,过点C作CE⊥AB,垂足为点E,点D为弧AC的中点,连接DE,如果DE=2OE,求线段AE的长.
小何根据学习函数的经验,将此问题转化为函数问题解决.
小华假设AE的长度为xcm,线段DE的长度为ycm.
(当点C与点A重合时,AE的长度为0cm),对函数y随自变量x的变化而变化的规律进行探究.
下面是小何的探究过程,请补充完整:(说明:相关数据保留一位小数).
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 |
| 5.8 | 5.7 |
当x=6cm时,请你在图中帮助小何完成作图,并使用刻度尺度量此时线段DE的长度,填写在表格空白处:
(2)在图2中建立平面直角坐标系,描出补全后的表中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象解决问题,当DE=2OE时,AE的长度约为 cm.