题目内容
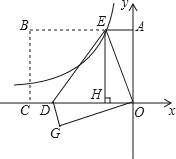
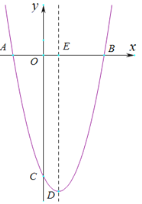
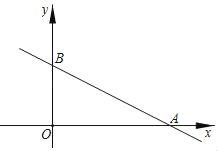
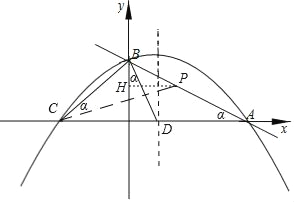
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+b与x轴相交于点A,与y轴相交于点B,抛物线y=ax2﹣4ax+4经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点 D.
x+b与x轴相交于点A,与y轴相交于点B,抛物线y=ax2﹣4ax+4经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点 D.
(1)求抛物线的表达式;
(2)求证:△BOD∽△AOB;
(3)如果点P在线段AB上,且∠BCP=∠DBO,求点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4(2)证明见解析(3)(
x+4(2)证明见解析(3)(![]() ,
,![]() )
)
【解析】
(1)利用直线表达式求出点A、B的坐标,把这两个点的坐标代入二次函数表达式即可求解;
(2)利用两个三角形夹角相等、夹边成比例,即可证明△BOD∽△AOB;
(3)证明△BCP∽△BAC,则![]() ,求出BP的长度,即可求解.
,求出BP的长度,即可求解.
解:(1)∵抛物线y=ax2﹣4ax+4经过点A和点B,点B在y轴上,
∴当x=0时,y=4,
∴点B的坐标为(0,4),
∵直线y=﹣![]() x+b与x轴相交于点A,与y轴相交于点B,
x+b与x轴相交于点A,与y轴相交于点B,
∴b=4,
∴直线y=﹣![]() x+4,
x+4,
当y=0时,x=8,
∴点A的坐标为(8,0),
∵抛物线y=ax2﹣4ax+4经过点A和点B,
∴a×82﹣4a×8+4=0,解得,a=![]() ,
,
∴抛物线y=![]() x2+
x2+![]() x+4;
x+4;
(2)证明:∵y=![]() x2+
x2+![]() x+4=
x+4=![]() +
+![]() ,该抛物线的对称轴与x轴相交于点D,
,该抛物线的对称轴与x轴相交于点D,
令y=0,解得:x=﹣4和8,则点C的坐标为(﹣4,0),即:OC=4,
∴点D的坐标为(2,0),∴OD=2,
∵点B(0,4),
∴OB=4,
∵点A(8,0),
∴OA=8,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠BOD=∠AOB=90°,
∴△BOD∽△AOB;
(3)连接CP,∵△BOD∽△AOB,
∴∠OBD=∠BAO=α,∠BCP=∠DBO=α,
∴∠BCP=∠BAO=α,而∠CPB=∠CBP,
∴△BCP∽△BAC,则![]() ,
,
其中,BC=4![]() ,AB=4
,AB=4![]() ,代入上式并解得:BP=
,代入上式并解得:BP=![]() ,
,
过点P作x轴的平行线交y轴于点H,
∵PH∥x轴,
∴![]() ,
,
即:![]() ,解得:PH=
,解得:PH=![]() ,
,
即:点P的横坐标为:![]() ,
,
同理可得其纵坐标为![]() ,
,
即点P的坐标为(![]() ,
,![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
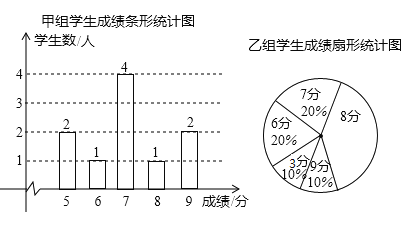
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.