题目内容
【题目】如图7所示,点![]() 、
、![]() 、
、![]() 在
在![]() 轴上,且
轴上,且![]() ,分别过点
,分别过点![]() 、
、![]() 、
、![]() 作
作![]() 轴的平行线,与反比例函数
轴的平行线,与反比例函数![]() 的图象分别交于点
的图象分别交于点![]() 、
、![]() 、
、![]() ,分别过点
,分别过点![]()
![]()
![]() 作
作![]() 轴的平行线,分别与
轴的平行线,分别与![]() 轴交于点
轴交于点![]()
![]()
![]() ,连接
,连接![]()
![]()
![]() ,那么图中阴影部分的面积之和为___________.
,那么图中阴影部分的面积之和为___________.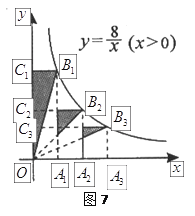
【答案】![]()
【解析】
先根据反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值得到S△OB1C1=S△OB2C2=S△OB3C3=![]() k=4,再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和.
k=4,再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和.
解答:解:根据题意可知S△OB1C1=S△OB2C2=S△OB3C3=![]() k=4
k=4
∵OA1=A1A2=A2A3,A1B1∥A2B2∥A3B3∥y轴
设图中阴影部分的面积从左向右依次为s1,s2,s3
则s1=![]() k=4,
k=4,
∵OA1=A1A2=A2A3,
∴s2:S△OB2C2=1:4,s3:S△OB3C3=1:9
∴图中阴影部分的面积分别是s1=4,s2=1,s3=![]()
∴图中阴影部分的面积之和=4+1+![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目