Question

【题目】如图，在正方形ABCD中，点M、N分别在AB、BC上，AB=4，AM=1，BN=.

(1)求证:ΔADM∽ΔBMN；

(2)求∠DMN的度数.

Answer 1

【答案】（1）见解析；（2）90°

【解析】

（1）根据，，即可推出，再加上∠A=∠B=90°，就可以得出△ADM∽△BMN；

（2）由△ADM∽△BMN就可以得出∠ADM=∠BMN，又∠ADM+∠AMD=90°，就可以得出∠AMD+∠BMN=90°，从而得出∠DMN的度数．

(1)∵AD=4，AM=1

∴MB=AB-AM=4-1=3

∵，

∴

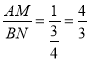
又∵∠A=∠B=90°

∴ΔADM∽ΔBMN

(2)∵ΔADM∽ΔBMN

∴∠ADM=∠BMN

∴∠ADM+∠AMD=90°

∴∠AMD+∠BMN=90°

∴∠DMN=180°-∠BMN-∠AMD=90°