题目内容
【题目】如图,已知抛物线y=﹣x2+2x经过原点O,且与直线y=x﹣2交于B,C两点.
(1)求抛物线的顶点A的坐标及点B,C的坐标;
(2)求证:∠ABC=90°;
(3)在直线BC上方的抛物线上是否存在点P,使△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(4)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.

【答案】(1) A(1,1), B(2,0),C(-1,-3);(2)证明见解析;(3) 存在满足条件的点P,( ![]() ,
,
![]() );(4) 存在满足条件的N点,其坐标为(5,0)或(-1,0)或(
);(4) 存在满足条件的N点,其坐标为(5,0)或(-1,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
);
【解析】(1)把抛物线解析式化为顶点式可求得A点坐标,联立抛物线与直线的解析式可求得B、C的坐标;
(2)由A、B、C的坐标可求得AB2、BC2和AC2,由勾股定理的逆定理可判定△ABC是直角三角形;
(3)过点P作PG∥y轴,交直线BC于点G,设出P点坐标,则可表示出G点坐标,从而可表示出PG的长,则可表示出△PBC的面积,利用二次函数的性质可求得其最大值时P点坐标;
(4)设出M、N的坐标,则可表示出MN和ON的长度,由相似三角形的性质可得到关于N点坐标的方程可求得N点坐标.
解:(1)∵y=﹣x2+2x=﹣(x﹣1)2+1,
∴抛物线顶点坐标A(1,1),
联立抛物线与直线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(2,0),C(﹣1,﹣3);
(2)证明:
由(1)可知B(2,0),C(﹣1,﹣3),A(1,1),
∴AB2=(1﹣2)2+12=2,BC2=(﹣1﹣2)2+(﹣3)2=18,
AC2=(﹣1﹣1)2+(﹣3﹣1)2=20,∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABC=90°;
(3)如图,过点P作PG∥y轴,交直线BC于点G,
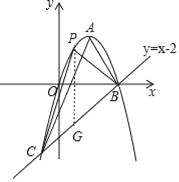
设P(t,﹣t2+2t),则G(t,t﹣2),
∵点P在直线BC上方,
∴PG=﹣t2+2t﹣(t﹣2)=﹣t2+t+2=﹣(t﹣![]() )2+,
)2+,
∴S△PBC=S△PGB+S△PGC=![]() PG[2﹣(﹣1)]=
PG[2﹣(﹣1)]= ![]() PG=﹣
PG=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=![]() 时,S△PBC有最大值,此时P点坐标为(
时,S△PBC有最大值,此时P点坐标为(![]() ,
, ![]() ),
),
即存在满足条件的点P,其坐标为(![]() ,
, ![]() );
);
(4)∵∠ABC=∠ONM=90°,
∴当△OMN和△ABC相似时,有![]() 或
或![]() ,
,
设N(m,0),
∵MN⊥x轴,
∴M(m,﹣m2+2m),
∴MN=|﹣m2+2m|,ON=|m|,
①当![]() 时,即
时,即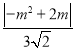 =
=![]() ,解得m=5或m=﹣1或m=0(舍去);
,解得m=5或m=﹣1或m=0(舍去);
②当![]() 时,即
时,即![]() =
=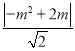 ,解得m=
,解得m=![]() 或m=
或m=![]() 或m=0(舍去);
或m=0(舍去);
综上可知存在满足条件的N点,其坐标为(5,0)或(﹣1,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
“点睛”此题考查了二次函数的综合应用,涉及了相似三角形的判定与性质、勾股定理,解答本题需要我们熟练各个知识点的内容,认真探究题目,谨慎作答.