题目内容
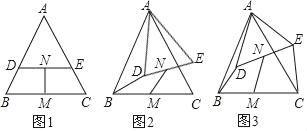
【题目】长为1,宽为a的矩形纸片(![]() ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )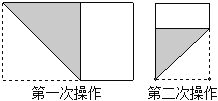
【答案】![]() 或
或![]() .
.
【解析】
根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当![]() <a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1-a,a.由1-a<a可知,第二次操作时所得正方形的边长为1-a,剩下的矩形相邻的两边分别为1-a,a-(1-a)=2a-1.由于(1-a)-(2a-1)=2-3a,所以(1-a)与(2a-1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1-a>2a-1;②1-a<2a-1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1-a,a.由1-a<a可知,第二次操作时所得正方形的边长为1-a,剩下的矩形相邻的两边分别为1-a,a-(1-a)=2a-1.由于(1-a)-(2a-1)=2-3a,所以(1-a)与(2a-1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1-a>2a-1;②1-a<2a-1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
解:由题意,可知当![]() <a<1时,第一次操作后剩下的矩形的长为a,宽为1-a,所以第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1.
<a<1时,第一次操作后剩下的矩形的长为a,宽为1-a,所以第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1.
故答案为1-a;
此时,分两种情况:
①如果1-a>2a-1,即a<![]() ,那么第三次操作时正方形的边长为2a-1.
,那么第三次操作时正方形的边长为2a-1.
∵经过第三次操作后所得的矩形是正方形,
∴矩形的宽等于1-a,
即2a-1=(1-a)-(2a-1),解得a=![]() ;
;
②如果1-a<2a-1,即a>![]() ,那么第三次操作时正方形的边长为1-a.
,那么第三次操作时正方形的边长为1-a.
则1-a=(2a-1)-(1-a),解得a=![]() .
.
综上所述:a的值是![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
功率 | 使用寿命 | 价格 | |
普通白炽灯 |
|
|
|
优质节能灯 |
|
|
|
已知这两种灯的照明效果一样,小明家所在地的电价是每度![]() 元.(注:用电度数
元.(注:用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时),费用
时间(小时),费用![]() 灯的售价
灯的售价![]() 电费);如:若选用一盏普通白炽灯照明
电费);如:若选用一盏普通白炽灯照明![]() 小时,那么它的费用为
小时,那么它的费用为![]() (元),请解决以下问题:
(元),请解决以下问题:
(1)在白炽灯的使用寿命内,设照明时间为![]() 小时,请用含
小时,请用含![]() 的代数式分别表示用一盏白炽灯的费用
的代数式分别表示用一盏白炽灯的费用![]() ,(元)和一盏节能灯的费用
,(元)和一盏节能灯的费用![]() (元);
(元);
(2)在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?
(3)如果计划照明![]() 小时,购买哪一种灯更省钱?请你通过计算说明理由.
小时,购买哪一种灯更省钱?请你通过计算说明理由.