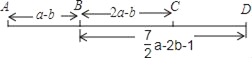Question

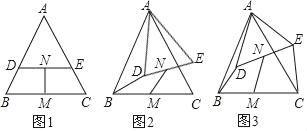
【题目】如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．

（1）发现：在图1中，=　 　；

（2）应用：如图2，将△ADE绕点A旋转，请求出的值；

（3）拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N分别是底边BC，DE的中点，若BD⊥CE，请直接写出的值．

Answer 1

【答案】(1);(2) ;(3) .

【解析】分析：（1）如图1中，作DH⊥BC于H，连接AM．只要证明四边形MNDH时矩形，即可解决问题；

（2）如图2中，连接AM、AN．只要证明△BAD∽△MAN，利用相似比为即可解决问题；

（3）如图3中，连接AM、AN，延长AD交CE于H，交AC于O．由△BAD∽△MAN，推出==sin∠ABC，只要证明△ABC时等腰直角三角形即可解决问题．

详解：（1）如图1中，作DH⊥BC于H，连接AM．

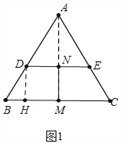
∵AB=AC，BM=CM，

∴AM⊥BC，

∵△ADE时等边三角形，

∴∠ADE=60°=∠B，

∴DE∥BC，

∵AM⊥BC，

∴AM⊥DE，

∴AM平分线段DE，

∵DN=NE，

∴A、N、M共线，

∴∠NMH=∠MND=∠DHM=90°，

∴四边形MNDH时矩形，

∴MN=DH，

∴==sin60°=，

故答案为．

（2）如图2中，连接AM、AN．

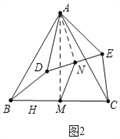
∵△ABC，△ADE都是等边三角形，BM=MC，DN=NE，

∴AM⊥BC，AN⊥DE，

∴=sin60°，=sin60°，

∴=，

∵∠MAB=∠DAN=30°，

∴∠BAD=∠MAN，

∴△BAD∽△MAN，

∴==sin60°=．

（3）如图3中，连接AM、AN，延长AD交CE于H，交AC于O．

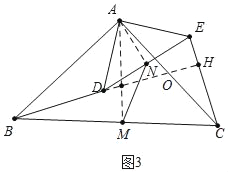
∵AB=AC，AD=AE，BM=CM，DN=NE，

∴AM⊥BC，AN⊥DE，

∵∠BAC=∠DAE，

∴∠ABC=∠ADE，

∴sin∠ABM=sin∠ADN，

∴=，

∵∠BAM=BAC，∠DAN=∠DAE，

∴∠BAM=∠DAN，

∴∠BAD=∠MAN．

∴△BAD∽△MAN，

∴==sin∠ABC，

∵∠BAC=∠DAE，

∴∠BAD=∠CAE，

∵AB=AC，AD=AE，

∴△BAD≌△CAE，

∴∠ABD=∠ACE，

∵BD⊥CE，

∴∠BHC=90°，

∴∠ACE+∠COH=90°，

∵∠AOB=∠COH，

∴∠ABD+∠AOB=90°，

∴∠BAO=90°，

∵AB=AC，

∴∠ABC=45°，

∴=sin45°=．