��Ŀ����
����Ŀ���Ķ�������ϣ��ش�����
�����ܹ���������
�ƴ�������ѧ�Һ�������ʫ�������С�������֣���ɫң����ȴ�ޣ�
����ӡ������ʫ��̩����ڡ���������ңԶ�ľ��롷��д����
����������ңԶ�ľ���
����˲�����Ѱ��
���������
��ע���������
��������ѧ������ѧ������ѧ�е����Ż��⣬Ψ�ж����������в��������������������߶ȣ�
��֪�� A��B �������Ϸֱ��ʾ������ a��b��A��B ����֮��ľ����ʾΪ AB��
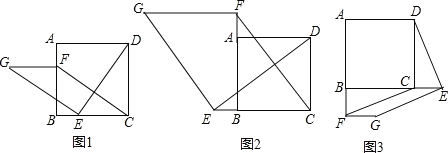
��![]() ���� A��B ��������һ����ԭ��ʱ��������� A ��ԭ�㣬��ͼ 1��
���� A��B ��������һ����ԭ��ʱ��������� A ��ԭ�㣬��ͼ 1��![]() ��
��
��![]() ���� A��B ���㶼����ԭ��ʱ��
���� A��B ���㶼����ԭ��ʱ��
����ͼ 2���� A��B ����ԭ����ұߣ�![]() ��
��
����ͼ 3���� A��B ����ԭ�����ߣ�![]() ��
��
����ͼ 4���� A��B ��ԭ������ߣ�![]() ��
��
���ϣ������� A��B ����ľ��� ![]() ��
��
�����������ۣ��ش������������⣺
![]()
��1���������ϱ�ʾ ![]() ��
��![]() ������֮��ľ�����
������֮��ľ�����![]() ����
���� ![]() ��
��
��2��������ʽ ![]() ȡ��Сֵʱ����
ȡ��Сֵʱ����![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��3����δ֪�� ![]() ��
��![]() ����
���� ![]() �������ʽ
�������ʽ ![]() �����ֵ�� ����Сֵ�� ��
�����ֵ�� ����Сֵ�� ��
���𰸡���1��-6��2����2��-1��x��2����3��7��-1��
��������
��1��������ת��Ϊ����ֵ���̣����ɽ�����⣮
��2��������ʽ|x+1|+|x-2|ȡ��Сֵʱ����ʾ����������һ��x����-1��2�ľ���֮����С����Ȼ�����x��-1��2֮�䣨����-1��2�����ɴ˼��ɽ�����⣮
��3������Ϊ��|x-1|+|x-3|����|y-2|+|y+1|��=6������Ϊ|x-1|+|x-3|����СֵΪ2��|y-2|+|y+1|����СֵΪ3������1��x��3��-1��y��2���ɴ˲��ѵõ��𰸣�
��1���������ϱ�ʾx��-2������֮��ľ�����4��
��|x+2|=4��
���x=-2-4=-6��x=-2+4=2��
�ʴ�Ϊ-6��2��
��2��������ʽ|x+1|+|x-2|ȡ��Сֵʱ����ʾ����������һ��x����-1��2�ľ���֮����С����Ȼ�����x��-1��2֮�䣨����-1��2����
��x��ȡֵ��Χ��-1��x��2��
�ʴ�Ϊ-1��x��2��
��3���ߣ�|x-1|+|x-3|����|y-2|+|y+1|��=6��
�֡�|x-1|+|x-3|����СֵΪ2��|y-2|+|y+1|����СֵΪ3��
��1��x��3��-1��y��2��
�����ʽx+2y�����ֵ��7����Сֵ��-1��
�ʴ�Ϊ7��-1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�