题目内容
【题目】四川是闻名天下的“熊猫之乡”,每年到大熊猫基地游玩的游客络绎不绝,大学生小张加入创业项目,项目帮助她在基地附近租店卖创意熊猫纪念品.已知某款熊猫纪念物成本为30元/件,当售价为45元/件时,每天销售250件,售价每上涨1元,销量下降10件.
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)若每天该熊猫纪念物的销售量不低于240件的情况下,当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
(3)小张决定从这款纪念品每天的销售利润中捐出150元给希望工程,为了保证捐款后这款纪念品每天剩余利润不低于3600元,试确定该熊猫纪念物销售单价的范围.
【答案】(1)为y=﹣10x+700;(2)46元时每天获取的利润最大利润是3840元;(3)45≤x≤55.
【解析】
(1)根据每上涨1元,销量下降10件即可求解;
(2)根据每天获得利润等于单件利润乘以销售量列出二次函数,再根据二次函数的性质即可求解;
(3)根据每天剩余利润不低于3600元和二次函数图象即可求解.
解:(1)根据题意,得
y=250﹣10(x﹣45)=﹣10x+700.
答:每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=﹣10x+700.
(2)销售量不低于240件,得﹣10x+700≥240
解得x≤46,
∴30<x≤46.
设销售单价为x元时,每天获取的利润是w元,根据题意,得
w=(x﹣30)(﹣10x+700)
=﹣10x2+1000x﹣21000
=﹣10(x﹣50)2+4000
∵﹣10<0,
所以x<50时,w随x的增大而增大,
所以当x=46时,w有最大值,
w的最大值为﹣10(46﹣50)2+4000=3840.
答:销售单价为46元时,每天获取的利润最大,最大利润是3840元.
(3)根据题意,得
w﹣150=﹣10x2+1000x﹣21000﹣150=3600
即﹣10(x﹣50)2=﹣250
解得x1=55,x2=45,
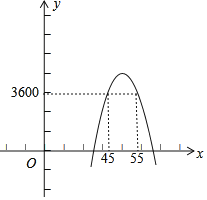
根据图象得,当45≤x≤55时,捐款后每天剩余利润不低于3600元.

【题目】为了解某校九年级学生阅读课外书籍的情况,某研究小组随机采访该校九年级的20位同学,得到这20位同学阅读课外书册数的统计信息,数据如下:
册数 | 0 | 2 | 3 | 5 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 8 | 2 | 2 | 1 |
(1)这20位同学阅读课外书册数的众数是 册,中位数是 册;
(2)若该校九年级有600名学生,试估计该校九年级学生阅读课外书的总册数.