题目内容
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 上一点,
上一点,![]() 于
于![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)当点![]() 在对角线
在对角线![]() (不含
(不含![]() 、
、![]() 两点)上运动时,
两点)上运动时,![]() 是否为定值?如果是,请求其值;如果不是,试说明理由.
是否为定值?如果是,请求其值;如果不是,试说明理由.
【答案】(1)证明见解析;(2)是定值,![]()
【解析】
(1)首先证明△AFE是等腰直角三角形,可得PF⊥AE,由直角三角形的性质可得结论;
(2)由“SAS”可证△APB≌△APD,可得PB=PD,通过证明△AFC∽△APB,可得![]() ,即可得
,即可得![]() .
.
解:(1)如图,连接PF,
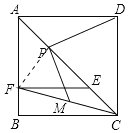
∵四边形ABCD是正方形
∴∠BAC=45°=∠CAD,AB=AD
∵EF⊥AB
∴∠BAC=∠AEF=45°
∴AF=EF,
∴△AFE是等腰直角三角形,且P是AE中点,
∴PF⊥AE,
∵点M是Rt△PFC斜边FC的中点
∴PM=![]() FC
FC
(2)是定值,
理由如下:如图,连接PB
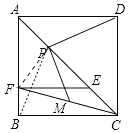
∵AP=AP,∠BAC=∠DAC=45°,AB=AD
∴△APB≌△APD(SAS)
∴PD=PB
∵△ABC,△AFE是等腰直角三角形
∴![]() ,
,![]()
∴![]() ,且∠BAP=∠FAC
,且∠BAP=∠FAC
∴△AFC∽△APB
∴![]()
∴![]()
∴![]()

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?