题目内容
【题目】如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.
(1)求证:AC∥OP;
(2)若∠APB=60°,BC=10cm,求AC的长.

【答案】(1)详见解析;(2)5cm.
【解析】试题分析:(1)根据切线性质得出![]() OP平分
OP平分![]() 推出
推出![]() 即
即![]() 由三角形外角的性质得出
由三角形外角的性质得出![]() 进而得出
进而得出![]() 根据平行线的判定推出即可;
根据平行线的判定推出即可;
(2)先求出![]() 为等边三角形,进而求出
为等边三角形,进而求出![]() 根据30°角的直角三角形性质求出即可.
根据30°角的直角三角形性质求出即可.
试题解析:(1)连接OA,
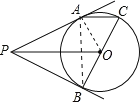
∵PA、PB分别切O于A.B,
∴OA⊥PA,OB⊥PB,
∵OP平分∠APB,
∴∠POA=∠POB,即∠BOA=2∠POB,
而∠BOA=2∠C,
∴∠POB=∠C,
∴AC∥OP.
(2)连接AB,∵PA、PB分别切O于A.B,
∴PA=PB.
又![]()
∴△PAB为等边三角形,
![]()
![]()
又∵BC为![]() 的直径,
的直径,
![]()
∵BC=10cm,
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目