题目内容
【题目】如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F.
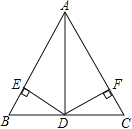
(1)请写出与A点有关的三个正确结论;
(2)DE与DF在数量上有何关系?并给出证明.
【答案】①AD⊥BC,②AD平分∠BAC,③AB=AC,④△ABE是等腰三角形,⑤△AED≌△AFD;(2) DE=DF.证明详见解析.
【解析】
(1)先运用勾股定理的逆定理证明△ABD为直角三角形,且∠ADB=90°,再运用勾股定理求出AC=5,则AB=AC,然后利用等腰三角形的性质即可求解;
(2)根据角平分线的性质即可得出DE=DF.
(1)AD⊥BC,∠BAD=∠CAD,AB=AC等.理由如下:
∵AB=5,AD=4,BD=3,
∴42+32=52.
∴△ABD为直角三角形,且∠ADB=90°.
∵CD=3,
∴AC=![]() ,
,
∴AB=AC,
又∵BD=CD,
∴AD⊥BC,∠BAD=∠CAD;
(2)DE=DF,理由如下:
∵∠BAD=∠CAD,DE⊥AB于E,DF⊥AC于点F,
∴DE=DF.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目