题目内容
【题目】已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.
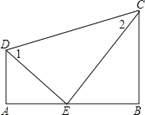
【答案】BC⊥AB.理由见解析
【解析】
根据角平分线的定义求出∠ADC=2∠1,∠BCD=2∠2,然后求出∠ADC+∠BCD=180°,再根据同旁内角互补,两直线平行求出AD∥BC,然后根据两直线平行,同旁内角互补求出∠B=90°,然后即可.
BC⊥AB.理由如下:
∵DE平分∠ADC,CE平分∠BCD,
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∵DA⊥AB,
∴∠A=90°,
∴∠B=180°∠A=180°90°=90°,
∴BC⊥AB.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
【题目】一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米):
+6 | - 5 | +9 | - 10 | +13 | - 9 | - 4. |
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共走了多少路程?




