题目内容
【题目】已知△ABC内接于⊙O,过点A作直线EF.
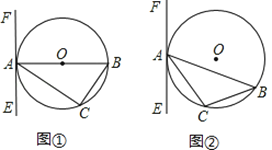
(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
【答案】(1)①∠BAE=90°,②∠EAC=∠ABC
(2)EF是⊙O的切线
【解析】试题分析:(1)若EF是切线,则AB⊥EF,添加的条件只要能使AB⊥EF即可;
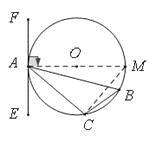
(2)作直径AM,连接CM,理由圆周角定理以及直径所对的圆周角是直角即可.
试题解析:(1)∠BAE=90°;∠CAE=∠B ;
EF是⊙O的切线.
作直径AM,连接CM,则∠ACM=90°,∠M=∠B,∴∠M+∠CAM=∠B+∠CAM=90°,∵∠CAE=∠B,∴∠CAM+∠CAE=90°,∴AE⊥AM,∵AM为直径,∴EF是⊙O的切线.

练习册系列答案
相关题目