题目内容
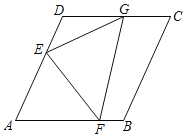
【题目】如图在菱形纸片ABCD中,AB=4,∠B=120°,将菱形纸片翻折,使点A落在边CD的中点G处,折痕为EF,点E,F分别在边AD,AB上,则sin∠GEF的值为_____.
【答案】![]()
【解析】
过点G作HG⊥AD于点H,连接AG交EF于点N,连接BD,BG.根据菱形的性质得到∠DAB=60°,AB=BC=CD=AD=4,∠DAB=∠DCB=60°,DC∥AB求得∠HDG=∠DAB=60°,根据线段中点的定义得到DG=![]() CD=2解直角三角形得到DH=1,HG=
CD=2解直角三角形得到DH=1,HG=![]() 求得AH=AD+DH=5,根据勾股定理得到EG=
求得AH=AD+DH=5,根据勾股定理得到EG=![]() ,AG=
,AG=![]() ,由折叠的性质得到AN=NG=
,由折叠的性质得到AN=NG=![]() ,AG⊥EF,于是得到结论.
,AG⊥EF,于是得到结论.
解:如图:过点G作HG⊥AD于点H,连接AG交EF于点N,连接BD,BG.
∵四边形ABCD是菱形,AB=4,∠ABC=120°,
∴∠DAB=60°,
∴AB=BC=CD=AD=4,∠DAB=∠DCB=60°,DC∥AB
∴∠HDG=∠DAB=60°,
∵点G是CD中点,
∴DG=![]() CD=2,
CD=2,
在Rt△DGH中,DG=2,∠HDG=60°
∴DH=1,HG=![]()
∴AH=AD+DH=5,
在Rt△EGH中,EG2=HG2+EH2,
∴EG2=(5﹣EG)2+3,
∴EG=![]() ,
,
在Rt△AHG中,AG=![]()
由折叠的性质的,AN=NG=![]() ,AG⊥EF,
,AG⊥EF,
∴sin∠GEF= ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校九年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,数据整理过程如下,请完成下面数据整理中的问题:
(1)收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m= ,n= ;
(3)分析数据
①若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人;
②现从甲班指定的3名学生(1男2女),乙班指定的2名学生(1男1女)中分别抽取1名学生去参加身体素质拓展训练,用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率.
【题目】某商场经市场调查,发现进价为40元的台灯每月的销售量y(台)与售价x(元)的相关信息如下:
售价x(元) | 50 | 60 | 70 | 80 | …… |
销售量y(台) | 200 | 180 | 160 | 140 | …… |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 函数,求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?