题目内容
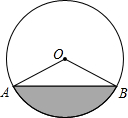
如图，A（0，6），C（1，0），H（0，1），且BH⊥AC．
（1）求点B的坐标；
（2）如图，若A，B，C在⊙M上，MN⊥BC于点N，求证：AH=2MN；
（3）以O为圆心，OA为半径作扇形OAB（如图），P为扇形OAB的
上异于A，B的动点，PE⊥OA于点E，PF⊥OB于点F，D，Q在EF上，且ED=DQ=QF．①当点P在
上运动时，在线段PE，PD，ED中，是否存在长度不变的线段？若存在，请求出该线段的长度，若不存在，请说明理由．②PE2+3PQ2的值是定值吗？若是，请求出这个定值，若不是，请说明理由．
（1）求点B的坐标；
（2）如图，若A，B，C在⊙M上，MN⊥BC于点N，求证：AH=2MN；
（3）以O为圆心，OA为半径作扇形OAB（如图），P为扇形OAB的
 |
| AB |
|
| AB |
（1）延长BH交AC于P，如图，
∵BH⊥AC，
∴∠HBO=∠OAC，
∵C（1，0），H（0，1），
∴OH=OC，
∴Rt△BOH≌Rt△AOC，
∴OB=OA，
而A（0，6），
∴B（-6，0）；
（2）⊙M交y轴于D，
过M点作MG⊥OA于G，如图，
∴∠DBC=∠DAC，
∴∠DBO=∠HBO，
∴OD=OH=1，
∴DG=AG=
DA=3.5，
∴OG=3.5-1=2.5，
而MN⊥BC，
∴四边形MNOG为矩形，
∴MN=OG=2.5，
又∵AH=AO-OH=6-1=5，
∴AH=2MN；
（3）
①存在长度不变的线段DE．
∵PE⊥OA，PF⊥OB于F，
∴四边形PEOF为矩形，线段PF和PE的长随P的变化而变化，
∴EF=OP=6，
而ED=DQ=QF，
∴DE=
EF=2；
②PE2+3PQ2的值是定值．
过Q作QC⊥PF于C，如图，
∴QC∥PE，
∴CQ：PE=FC：FP=FQ：FE=1：3，
∴CQ=
PE，CF=
PF，
∴PC=
PF，
在Rt△PCQ中，PQ2=PC2+CQ2，
∴PQ2=
PF2+
PE2，
∴PE2+3PQ2=PE2+
PF2+
PE2=
（PF2+PE2）=
EF2=
×62=48．
∵BH⊥AC，
∴∠HBO=∠OAC，
∵C（1，0），H（0，1），
∴OH=OC，
∴Rt△BOH≌Rt△AOC，
∴OB=OA，
而A（0，6），
∴B（-6，0）；
（2）⊙M交y轴于D，
过M点作MG⊥OA于G，如图，∴∠DBC=∠DAC，
∴∠DBO=∠HBO，
∴OD=OH=1，
∴DG=AG=
| 1 |
| 2 |
∴OG=3.5-1=2.5，
而MN⊥BC，
∴四边形MNOG为矩形，
∴MN=OG=2.5，
又∵AH=AO-OH=6-1=5，
∴AH=2MN；
（3）
①存在长度不变的线段DE．∵PE⊥OA，PF⊥OB于F，
∴四边形PEOF为矩形，线段PF和PE的长随P的变化而变化，
∴EF=OP=6，
而ED=DQ=QF，
∴DE=
| 1 |
| 3 |
②PE2+3PQ2的值是定值．
过Q作QC⊥PF于C，如图，
∴QC∥PE，
∴CQ：PE=FC：FP=FQ：FE=1：3，
∴CQ=
| 1 |
| 3 |
| 1 |
| 3 |
∴PC=
| 2 |
| 3 |
在Rt△PCQ中，PQ2=PC2+CQ2，
∴PQ2=
| 4 |
| 9 |
| 1 |
| 9 |
∴PE2+3PQ2=PE2+
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
练习册系列答案
相关题目
