Question

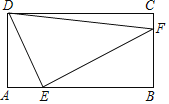
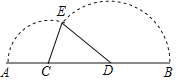
【题目】在矩形ABCD中，AB＝3，AD＝5，E是射线DC上的点，连接AE，将△ADE沿直线AE翻折得△AFE．

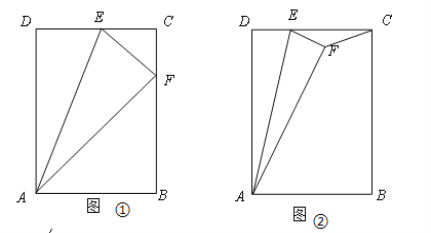
（1）如图①，点F恰好在BC上，求证：△ABF∽△FCE；

（2）如图②，点F在矩形ABCD内，连接CF，若DE＝1，求△EFC的面积；

（3）若以点E、F、C为顶点的三角形是直角三角形，则DE的长为 ．

Answer 1

【答案】（1）证明见解析；（2）；（3）、5、15、

【解析】

（1）利用同角的余角相等，证明∠CEF＝∠AFB，即可解决问题;（2）过点F作FG⊥DC交DC与点G，交AB于点H,由△FGE∽△AHF得出AH=5GF，再利用勾股定理求解即可;（3）分①当∠EFC=90°时; ②当∠ECF=90°时;③当∠CEF=90°时三种情况讨论解答即可.

（1）解：在矩形ABCD中，∠B＝∠C＝∠D＝90°

由折叠可得：∠D＝∠EFA＝90°

∵∠EFA＝∠C＝90°

∴∠CEF＋∠CFE＝∠CFE＋∠AFB＝90°

∴∠CEF＝∠AFB

在△ABF和△FCE中

∵∠AFB＝∠CEF，∠B＝∠C＝90°

△ABF∽△FCE

（2）解：过点F作FG⊥DC交DC与点G，交AB于点H，则∠EGF＝∠AHF＝90°

在矩形ABCD中，∠D＝90°

由折叠可得：∠D＝∠EFA＝90°，DE＝EF＝1，AD＝AF＝5

∵∠EGF＝∠EFA＝90°

∴∠GEF＋∠GFE＝∠AFH＋∠GFE＝90°

∴∠GEF＝∠AFH

在△FGE和△AHF中

∵∠GEF＝∠AFH，∠EGF＝∠FHA＝90°

∴△FGE∽△AHF

∴＝

∴＝

∴AH=5GF

在Rt△AHF中，∠AHF＝90°

∵AH2＋FH2=AF2

∴（5 GF）2＋（5 －GF）2=52

∴GF＝

∴△EFC的面积为××2＝ ;

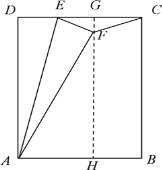
（3）解：①当∠EFC=90°时，A、F、C共线，如图所示:

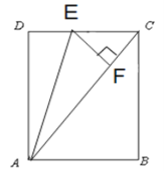
设DE=EF=x,则CE=3-x,

∵AC=,∴CF=-x, ∵∠CFE=∠D=90°, ∠DCA=∠DCA, ∴△CEF∽△CAD, ∴,即，解得:ED=x=;

②当∠ECF=90°时,如图所示:

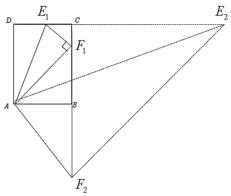
∵AD==5,AB=3, ∴==4, 设=x,则=3-x,∵∠DCB=∠ABC=90°,

∴∽,∴,即，解得:x==;

由折叠可得 : ,设，则，,

在RT△中，

∵,即9+x=(x+3),解得x==12, ∴;

③当∠CEF=90°时，AD=AF,此时四边形AFED是正方形，∴AF=AD=DE=5,

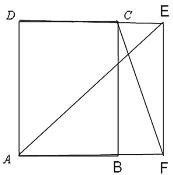
综上所述，DE的长为:、5、15、.