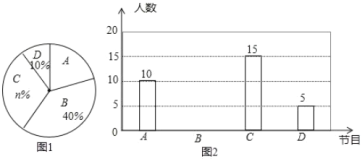
��Ŀ����
����Ŀ���Ķ����в��ϣ��������������⣮
���ϣ������Ĵ�ʼ�����ո�����ѧ����Ƥ����J��Npler��1550-1617�꣩����Ƥ��������������ָ����д��ʽ֮ǰ��ֱ��18������ʿ��ѧ��ŷ����Evler��1707-1783���ŷ���ָ�������֮�����ϵ������֪����n����ͬ������a���![]() ��Ϊ
��Ϊ![]() ����
����![]() ����ʱ��3������2Ϊ��8�Ķ�������Ϊ
����ʱ��3������2Ϊ��8�Ķ�������Ϊ![]() ����
����![]() ��
��
һ��أ���![]() ��
��![]() ��
��![]() ��
��![]() ������n������aΪ��b�Ķ�������Ϊ
������n������aΪ��b�Ķ�������Ϊ![]() ����
����![]() ����
����![]() ����4������3Ϊ��81�Ķ�������Ϊ
����4������3Ϊ��81�Ķ�������Ϊ![]() ����
����![]() ��
��
��1���������и�������ֵ��![]() ________��
________��![]() ________��
________��![]() ________��
________��
��2��ͨ���۲죨1��������![]() ��
��![]() ��
��![]() ֮������Ĺ�ϵʽ��________��
֮������Ĺ�ϵʽ��________��
��3����չ���죻�������һ���ԵĽ��۳�����������֤��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
֤������![]() ��
��![]() ��
��
�ɶ����Ķ���ã�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��.
��.
��4�����գ�3����֤��������֤�������һ���Խ�����
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��.
��.
��5�����㣺![]() ��ֵΪ________________.
��ֵΪ________________.
���𰸡�(1) 2��4��6;(2) ![]() +
+![]() =
=![]() ;(4)֤������⣻��5��1
;(4)֤������⣻��5��1
��������
��1�������������ָ��ʽ![]() ��
��![]() ��
��![]() �ɼ�����Ӧ������ֵ��
�ɼ�����Ӧ������ֵ��
��2����2+4=6��![]() ��
��![]() ��
��![]() �ɵ�
�ɵ�![]() +
+![]() =
=![]() ��
��
��4����![]() =m��
=m��![]() =n����M=
=n����M=![]() ��N=
��N=![]() ���ó�
���ó�![]() =
=![]() ���ɶ����Ķ����m-n=
���ɶ����Ķ����m-n=![]() ������֤�����ۣ�
������֤�����ۣ�
��5�����ݵó��Ķ��������ʣ���![]() =
=![]() ���ٽ��м��㼴�ɽ����.
���ٽ��м��㼴�ɽ����.
�⣺��1����![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ʴ��� :2��4��6
��2����2+4=6��![]() ��
��![]() ��
��![]()
��![]() +
+![]() =
=![]()
�ʴ��![]() +
+![]() =
=![]()
��4����![]() ��
��![]() ����
����![]() ��
��![]()
![]() ��
��
�ɶ����Ķ����![]()
��![]()
��![]()
��5��ԭʽ=![]()
=![]()
=1
�ʴ���:1