题目内容
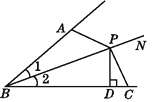
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

【答案】(1)①∠COP=∠BOP、②∠AOD=∠COB;(2)155°;(3)平分,理由见解析.
【解析】
(1)根据角平分线的性质和对顶角来填空;
(2)根据对顶角相等、角平分线的性质求得∠COP=![]() ∠AOD=25°;即可求出∠DOP的度数.
∠AOD=25°;即可求出∠DOP的度数.
(3)根据同角的余角相等得到∠EOC=∠BOF.根据角平分线的定义∠POC=∠POB,求得∠EOP=∠FOP.即可说明OP平分∠EOF.
(1)①∵OP是∠BOC的平分线,
∴∠COP=∠BOP.
②∵直线AB与CD相交于点O,
∴∠AOD=∠COB.
故答案是:∠COP=∠BOP、∠AOD=∠COB;
(2)∵∠AOD=∠BOC=50°,OP是∠BOC的平分线,
∴∠COP=![]() ∠AOD=25°.
∠AOD=25°.
∴∠DOP=180°-25°=155°;
(3)平分,理由如下:
∵如图,OE⊥AB,OF⊥CD,
∴∠EOB=90°,∠COF=90°,
∴∠EOB=∠COF,
∴∠EOC=∠BOF.
∵OP是∠BOC的平分线,
∴∠POC=∠POB,
∴∠EOP=∠FOP,
∴OP平分∠EOF.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目