题目内容
【题目】已知抛物线![]() 与
与![]() 轴的两个交点是点
轴的两个交点是点![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴的交点是点
轴的交点是点![]() .
.
(1)求证:![]() ,
,![]() 两点中必有一个点坐标是
两点中必有一个点坐标是![]() ;
;
(2)若抛物线的对称轴是![]() ,求其解析式;
,求其解析式;
(3)在(2)的条件下,抛物线上是否存在一点![]() ,使
,使![]() ?如果存在,求出点
?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将抛物线表达式变形为![]() ,求出与x轴交点坐标即可证明;
,求出与x轴交点坐标即可证明;
(2)根据抛物线对称轴的公式,将![]() 代入即可求得a值,从而得到解析式;
代入即可求得a值,从而得到解析式;
(3)分点P在AC上方和下方两种情况,结合∠ACO=45°得出直线PC与x轴所夹锐角度数,从而求出直线PC解析式,继而联立方程组,解之可得答案.
解:(1)![]() =
=![]() ,
,
令y=0,则![]() ,
,![]() ,
,
则抛物线与x轴的交点中有一个为(-2,0);
(2)抛物线的对称轴是:![]() =
=![]() ,
,
解得:![]() ,代入解析式,
,代入解析式,
抛物线的解析式为:![]() ;
;
(3)存在这样的点![]() ,
,
![]() ,
,
![]() ,
,
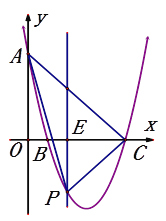
如图1,当点![]() 在直线
在直线![]() 上方时,记直线
上方时,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
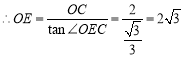 ,
,
则![]() ,
,![]() ,
,
求得直线![]() 解析式为
解析式为![]() ,
,
联立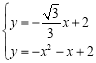 ,
,
解得![]() 或
或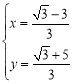 ,
,
![]() ,
,![]() ;
;
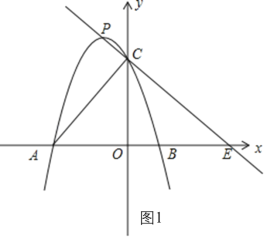
如图2,当点![]() 在直线
在直线![]() 下方时,记直线
下方时,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
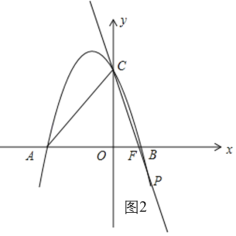
![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
求得直线![]() 解析式为
解析式为![]() ,
,
联立![]() ,
,
解得:![]() 或
或![]() ,
,
![]() ,
,![]() ,
,
综上,点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.

练习册系列答案
相关题目