题目内容
【题目】在平面直角坐标系中，抛物线
与y轴的交点为A，与x轴的正半轴分别交于点B（b，0），C（c，0）.
（1）当b=1时，求抛物线相应的函数表达式；
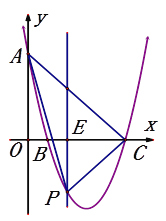
（2）当b=1时，如图，E（t，0）是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P．求△APC面积的最大值；
（3）当c =b+ n.时，且n为正整数.线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值.
【答案】(1)y=
﹣6x+5；(2)当t=
时，面积S有最大值
；(3)1或
．
【解析】试题分析：（1）当b=1时，将点B（1，0）代入抛物线y=﹣6mx+5中求出m，即可解决问题．
（2）如图1中，直线AC与PE交于点F．切线直线AC的解析式，构建二次函数，利用二次函数的性质即可解决问题．
（3）分两种情形①当b整数时，n为整数，可知n=4，c=b+4．则b，b+4是方程x2﹣mx+5=0的两个根，分别代入方程中求解即可，②当b小数时，n为整数，∴n=5，c=b+5为小数，则b，b+5是方程﹣6x+5=0的两个根.
试题解析：（1）当b=1时，将点B（1，0）代入抛物线y=﹣6mx+5中，得m=1，
∴y=﹣6x+5；
（2）如图1中，直线AC与PE交于点F．
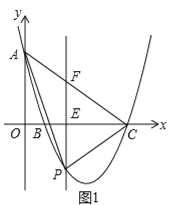
当b=1时，求得A（0，5），B（1，0），C（5，0），可得AC所在的一次函数表达式为y=﹣x+5，
∵E（t，0），
∴P （t，
﹣6t+5），直线l与AC的交点为F（t，﹣t+5），
∴PF=（﹣t+5）﹣（﹣6t+5）=
+5t，
∴
=
=
，
∵
＜0，
∴当t=时，面积S有最大值；
（3）①当b整数时，n为整数，
∴n=4，c=b+4．则b，b+4是方程﹣mx+5=0的两个根，分别代入方程中，
得
﹣mb+5=0①，
②，
由①②可得+4b﹣5=0，解得b=1或﹣5（舍）；
或由一元二次方程根与系数的关系得 b（b+4）=5解得b=1或﹣5（舍）．
②当b小数时，n为整数，∴n=5，c=b+5为小数，则b，b+5是方程﹣mx+5=0的两个根，同样可得b=或
（舍弃）；
∴b=1或．
