题目内容
【题目】作⊙O的内接正六边形ABCDEF,甲、乙两人的作法分别是:
甲:第一步:在⊙O上任取一点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F. 第二步:依次连接这六个点.
乙:第一步:任作一直径AD. 第二步:分别作OA,OD的中垂线与⊙O相交,交点从点A开始,依次为点B,C,E,F. 第三步:依次连接这六个点.
对于甲、乙两人的作法,可判断( )
A.甲正确,乙错误B.甲、乙均错误
C.甲错误,乙正确D.甲、乙均正确
【答案】D
【解析】
根据等边三角形的判定与性质,正六边形的定义解答即可.
(1)如图1,由作法知,△AOB, △BOC, △COD,△DOE,△EOF,△AOF都是等边三角形,
∴∠ABO=∠CBO=60°,
∴∠ABC=120°,
同理可证:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=∠FAB=120°,
∵AB=BC=CD=DE=EF=AF,
∴六边形ABCDEF是正六边形,
故甲正确;
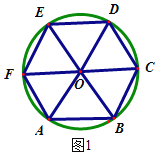
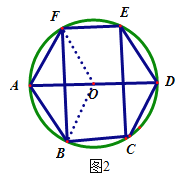
(2)如图2,连接OB,OF,
由作法知,OF=AF,AB=OB,
∵OA=OF=OB,
∴△AOF,△AOB是等边三角形,
∴∠OAF=∠OAB=60°,AB=AF,
∴∠BAF=120°,
同理可证,∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=∠FAB=120°,AB=BC=CD=DE=EF=AF,
∴六边形ABCDEF是正六边形,
故乙正确.
故选D.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目