题目内容
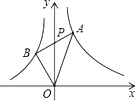
【题目】如图,![]() 的顶点A在双曲线
的顶点A在双曲线![]() 上,顶点B在双曲线
上,顶点B在双曲线![]() 上,AB中点P恰好落在y轴上,则
上,AB中点P恰好落在y轴上,则![]() 的面积为_____.
的面积为_____.
【答案】7
【解析】
过A作AE⊥y轴于E,过B作BD⊥y轴于D,得到∠AED=∠BDP=90°,根据全等三角形的性质得到S△BDP=S△AED,根据反比例函数系数k的几何意义得到S△OBD=3,S△AOE=4,于是得到结论.
解:过A作AE⊥y轴于E,过B作BD⊥y轴于D,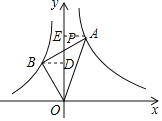
∴∠AED=∠BDP=90°,
∵点P是AB的中点,
∴BP=AP,
∵∠BPD=∠APE,
∴△BPD≌△APE(AAS),
∴S△BDP=S△AED,
∵顶点A在双曲线![]() ,顶点B在双曲线
,顶点B在双曲线![]() 上,
上,
∴S△OBD=3,S△AOE=4,
∴△OAB的面积=S△OBD+S△AOE=7,
故答案为:7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目