Question

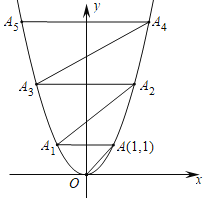
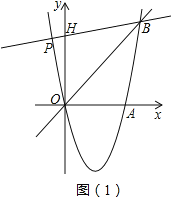
【题目】如图（1），二次函数y＝ax2﹣bx（a≠0）的图象与x轴、直线y＝x的交点分别为点A(4，0)、B(5，5)．

（1）a＝　 　，b＝　 　，∠AOB＝　 　°；

（2）连接AB，点P是抛物线上一点（异于点A），且∠PBO＝∠OBA，求点P的坐标　 　；

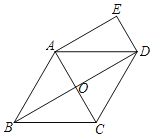
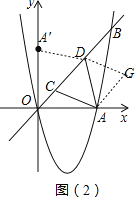
（3）如图（2），点C、D是线段OB上的动点，且CD＝2．设点C的横坐标为m．

①过点C、D分别作x轴的垂线，与抛物线相交于点F、E，连接EF．当CF+DE取得最大值时，求m的值并判断四边形CDEF的形状；

②连接AC、AD，求m为何值时，AC+AD取得最小值，并求出这个最小值．

Answer 1

【答案】（1）1，4，45°；（2）(﹣，)；（3）①m＝，四边形CDEF为平行四边形；②m=，2

【解析】

（1）将点A、B的坐标代入二次函数表达式，即可求解；

（2）证明△HOB≌△AOB（AAS），得OA＝OH＝4，即点H（0，4），即可求解；

（3）①则CF+DE＝m﹣m2+4m+（m+2）﹣[（m+2）2﹣4（m+2）]＝﹣2m2+6m+6，即可求解；

②如图所示，过点A作CD的平行线，过点D作AC的平行线，交于点G，则四边形ACDG是平行四边形，当A'、D、G三点共线时，A'D+DG＝A'G最短，即可求解．

（1）将点A、B的坐标代入二次函数表达式得：，解得：，

故二次函数表达式为：y＝x2+4x，

∵点O，B在直线y=x上，

∴OB平分∠xOy,

∴∠AOB=45；

故：答案为：1，4，45°；

（2）设直线BP交y轴于点H，

∵∠HOB＝∠AOB＝45°，∠PBO＝∠OBA，BO＝BO，

∴△HOB≌△AOB（AAS），

∴OA＝OH＝4，即点H（0，4），

则直线PB的表达式为：y＝kx+4，将点B坐标代入上式并解得：

直线PB的表达式为：y＝x+4，

将上式与二次函数表达式联立并解得：x＝5或﹣（舍去正值），

则点P（﹣，）；

（3）①由题意得：直线OB的表达式为：y＝x，

设点C（m，m），CD＝2，直线OB的倾斜角为45度，则点D（m+2，m+2），

则点F（m，m2﹣4m），点E[（m+2），（m+2）2﹣4（m+2）]，

则CF+DE＝m﹣m2+4m+（m+2）﹣[（m+2）2﹣4（m+2）]＝﹣2m2+6m+6，

∵﹣2＜0，故CF+DE有最大值，此时，m＝，

则点C、F、D、E的坐标分别为（，）、（，﹣）、（，）、（，﹣），

则CF＝DE＝，CF∥ED，

故四边形CDEF为平行四边形；

②如图所示，过点A作CD的平行线，过点D作AC的平行线，交于点G，则四边形ACDG是平行四边形，

∴AC＝DG，

作点A关于直线OB的对称点A'（0，4），连接A'D，则A'D＝AD，

∴当A'、D、G三点共线时，A'D+DG＝A'G最短，此时AC+AD最短，

∵A（4，0），AG＝CD＝2，

则点G（6，2），

则AC+AD最小值＝A'G＝＝2；