题目内容
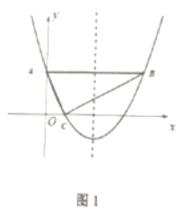
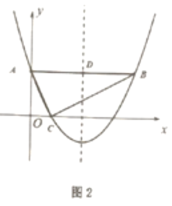
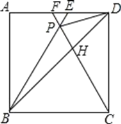
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①![]() ;②△DFP△BPH;③
;②△DFP△BPH;③![]() ; ④
; ④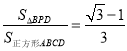 .其中正确的是______.(写出所有正确结论的序号).
.其中正确的是______.(写出所有正确结论的序号).
【答案】②③
【解析】
依据∠FDP=∠PBD,∠DFP=∠BPC=60°,即可得到△DFP∽△BPH,![]() ,判定△DPH∽△CPD,可得
,判定△DPH∽△CPD,可得![]() ,即PD2=PHCP,再根据CP=CD,即可得出PD2=PHCD;根据三角形面积计算公式,结合图形得到△BPD的面积=△BCP的面积+△CDP面积-△BCD的面积,即可得出
,即PD2=PHCP,再根据CP=CD,即可得出PD2=PHCD;根据三角形面积计算公式,结合图形得到△BPD的面积=△BCP的面积+△CDP面积-△BCD的面积,即可得出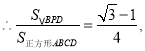
解:∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,故②正确;
∴![]()
故①不正确;
∵PC=DC,∠DCP=30°,
∴∠CDP=75°,
又∵∠DHP=∠DCH+∠CDH=75°,
∴∠DHP=∠CDP,而∠DPH=∠CPD,
∴△DPH∽△CPD,
∴![]() ,即PD2=PHCP,
,即PD2=PHCP,
又∵CP=CD,
∴PD2=PHCD,故③正确;
如图,过P作PM⊥CD,PN⊥BC,
设正方形ABCD的边长是4,△BPC为正三角形,则正方形ABCD的面积为16,
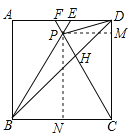
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
![]()
![]()
![]()
![]()
![]()
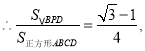 故④错误;
故④错误;
故答案为:②③

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案【题目】国家卫生健康委员会公布,截止4月2日全国疫情现存趋势图如下:

(1)结合图象,小彤对全国疫情做出以下四个判断:
①现存疑似病例与现存确诊病例数量差距最大日期大约出现在2月上旬;
②疫情在3月30日已经得到完全的控制;
③现存疑似人数大约在2月8日前后达到峰值;
④全国现存确诊病例人数3月底增加趋缓.
你认为判断正确的有________.
(2)针对这次疫情,某校初三一班的同学以小组为单位组织了“抗战疫情,我为湖北鼓劲”绘画活动.通过网络发往湖北,右图是同学们的上交绘画作品情况,结合统计图,回答:![]() ________,
________,![]() ________.
________.

(3)全国各地都向湖北伸出援助之手,其中北京市派遣医务人员前往较为严重的武汉和黄冈.请依据表格回答下列问题:
北京派遣至武汉、黄冈各医院医护人员对比表 | ||||||
武汉 | ||||||
5 | 7 | 9 | 12 | 11 | 8 | 19 |
20 | 7 | 7 | 3 | 1 | 20 | 13 |
黄冈 | ||||||
3 | 8 | 5 | 10 | 14 | 20 | |
4 | 2 | 9 | 18 | 11 | 15 | |
注:表格内的数字代表派遣至每个医院的医护人员人数 | ||||||
①派往武汉各医院医护人员的众数是________人;
②派黄冈各医院医护人员的平均数约是________人(四舍五入取整数);
③请你根据表格信息,判断两个地区哪里的疫情较为严重,说明理由.
【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.