题目内容
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
(1)求y与x的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.

【答案】(1)y与x的函数解析式为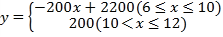 ;(2)这一天销售西瓜获得利润的最大值为1250元.
;(2)这一天销售西瓜获得利润的最大值为1250元.
【解析】
(1)当6![]() x≤10时,由题意设y=kx+b(k=0),利用待定系数法求得k、b的值即可;当10<x≤12时,由图象可知y=200,由此即可得答案;
x≤10时,由题意设y=kx+b(k=0),利用待定系数法求得k、b的值即可;当10<x≤12时,由图象可知y=200,由此即可得答案;
(2))设利润为w元,当6≦x≤10时,w=-200![]() +1250,根据二次函数的性质可求得最大值为1250;当10<x≤12时,w=200x-1200,由一次函数的性质结合x的取值范围可求得w的最大值为1200,两者比较即可得答案.
+1250,根据二次函数的性质可求得最大值为1250;当10<x≤12时,w=200x-1200,由一次函数的性质结合x的取值范围可求得w的最大值为1200,两者比较即可得答案.
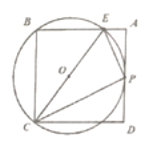
(1)当6![]() x≤10时,由题意设y=kx+b(k=0),它的图象经过点(6,1000)与点(10,200),
x≤10时,由题意设y=kx+b(k=0),它的图象经过点(6,1000)与点(10,200),
∴![]() ,
,
解得![]() ,
,
∴当6![]() x≤10时, y=-200x+2200,
x≤10时, y=-200x+2200,
当10<x≤12时,y=200,
综上,y与x的函数解析式为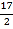 ;
;
(2)设利润为w元,
当6![]() x≤10时,y=-200x+2200,
x≤10时,y=-200x+2200,
w=(x-6)y=(x-6)(-200x+200)=-200![]() +1250,
+1250,
∵-200<0,6≦x≤10,
当x=![]() 时,w有最大值,此时w=1250;
时,w有最大值,此时w=1250;
当10<x≤12时,y=200,w=(x-6)y=200(x-6)=200x-1200,
∴200>0,
∴w=200x-1200随x增大而增大,
又∵10<x≤12,
∴当x=12时,w最大,此时w=1200,
1250>1200,
∴w的最大值为1250,
答:这一天销售西瓜获得利润的最大值为1250元.

 阅读快车系列答案
阅读快车系列答案