题目内容
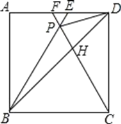
【题目】在平面直角坐标系中,![]() ,
,![]() ,
,![]() 轴,如图1,
轴,如图1,![]() ,且
,且![]()
![]() .
.
(1)![]() 点坐标为__________,
点坐标为__________,![]() 点坐标为__________;
点坐标为__________;
(2)求过![]() 、
、![]() 、
、![]() 三点的抛物线表达式;
三点的抛物线表达式;
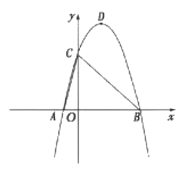
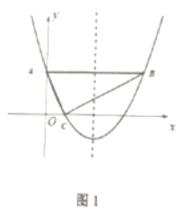
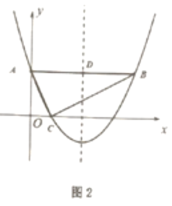
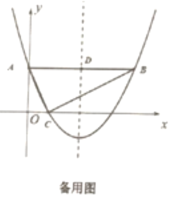
(3)如图2,抛物线对称轴与![]() 交于点
交于点![]() ,现有一点
,现有一点![]() 从点
从点![]() 出发,以每秒1个单位的速度在
出发,以每秒1个单位的速度在![]() 上向点
上向点![]() 运动,另一点
运动,另一点![]() 从点
从点![]() 与点
与点![]() 同时出发,以每秒5个单位在抛物线对称轴上运动.当点
同时出发,以每秒5个单位在抛物线对称轴上运动.当点![]() 到达
到达![]() 点时,点
点时,点![]() 、
、![]() 同时停止运动,问点
同时停止运动,问点![]() 、
、![]() 运动到何处时,
运动到何处时,![]() 面积最大,试求出最大面积.
面积最大,试求出最大面积.
【答案】(1)![]() ;(2)
;(2) ![]() (3) 当点
(3) 当点![]() 坐标为
坐标为![]() 点
点![]() 坐标为
坐标为![]() 或
或![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]()
【解析】
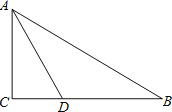
(1)由C(1,0)得OC=1,由![]() 1:2得OA=2,即A(0,2),由勾股定理求出AC的长,过点B 作BE⊥x轴,证明△ACO∽△CBE,可得BE,CE的长,从而可得结论;
1:2得OA=2,即A(0,2),由勾股定理求出AC的长,过点B 作BE⊥x轴,证明△ACO∽△CBE,可得BE,CE的长,从而可得结论;
(2)设抛物线表达式为y=ax2+bx+c,把A、B、C三点坐标代入,求解方程组得到a、b、c的值即可;
(3)根据题意求出BP=5-t,DQ=5t,结合三角形面积公式可得到![]() ,求出其最大值时即可得出P、Q坐标.
,求出其最大值时即可得出P、Q坐标.
(1)∵C(1,0),
∴OC=1,
∵![]() 1:2.
1:2.
∴OA=2,
∴A(0,2),
∴AC=![]() ,
,
∵![]() ,
,
∴BC=2![]() ,
,
过点B 作BE⊥x轴,垂足为点E,如图,

∵∠ACB=90°,
∴∠ACO+∠BCE=90°,
∵∠OAC+∠ACO=90°,
∴∠OAC=∠BCE,
又∠AOC=∠BEC=90°,
∴△ACO∽△CBE,
∴![]() ,
,
∴CE=4,BE=2,
∴OE=OC+CE=5,
∴B(5,0),
故答案为:![]() ,
,![]() ;
;
(2)设过![]() 、
、![]() 、
、![]() 三点的抛物线表达式为y=ax2+bx+c,
三点的抛物线表达式为y=ax2+bx+c,
把A(0,2)、B(5,2)、C(1,0)三点坐标代入,得:
 ,
,
解得, ,
,
所以,过![]() 、
、![]() 、
、![]() 三点的抛物线表达式为:
三点的抛物线表达式为:![]() ;
;
(3)解:在Rt△ABC中,BC=2![]() ,AC=
,AC=![]() ,∠ACB=90°,
,∠ACB=90°,
所以,AB=![]() ,
,
设运动![]() 秒时,
秒时,![]() 面积最大,且
面积最大,且![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() 当
当 时,
时,
面积最大值![]() ,
,
![]() 此时点
此时点![]() 坐标为
坐标为![]() ,
,
![]() 当点
当点![]() 向上运动时,
向上运动时,![]() 点坐标为
点坐标为![]()
当点![]() 向下运动时,
向下运动时,![]() 点坐标为
点坐标为![]()
![]() 综上所述,当点
综上所述,当点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 或
或![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案