Question

【题目】如图，直线与轴交于点，与轴交于点，抛物线经过、两点.

①求点的坐标；

②求抛物线的解析式；

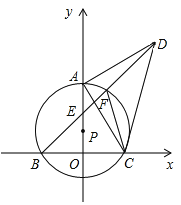
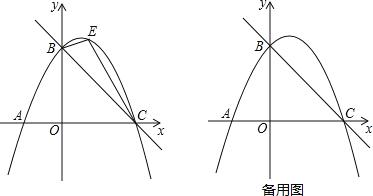
③如图，点是直线上方抛物线上的一动点，当面积最大时，请求出点的坐标和面积的最大值.

Answer 1

【答案】①；②；③点的坐标是时，的面积最大，最大面积是.

【解析】

①利用利用x轴上点的坐标特点代入一次函数即可.

②根据抛物线经过、两点，先求出B点坐标，再用待定系数法求解析式即可.

③根据“铅垂高，水平宽”方法求面积.过点作轴的平行线交直线于点，交轴于点，利用E、M横坐标相等及所在函数关系式设出坐标，求出EM的长，再利用，把EM看作△BEM和△MEC的底，求出面积写出关系式，最后利用二次函数求最值即可.

解：①∵直线与轴交于点，

∴当y=0时，解得x=4

∴C点坐标为：

②直线与轴交于点，与轴交于点，

当x=0时，解得y=3

∴点的坐标是，点的坐标是，

抛物线经过、两点，

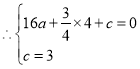
解得,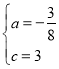

抛物线的解析式为.

③如图，过点作轴的平行线交直线于点，交轴于点，

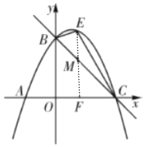
已知点是直线上方抛物线上的一动点，则可设点的坐标是，

点的坐标是，

.

，

.

即当时，即点的坐标是时，的面积最大，最大面积是.